#include <AlphaDivision.h>
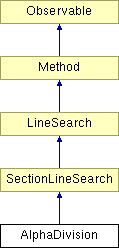
Diagram dziedziczenia dla AlphaDivision

Metoda optymalizacji w kierunku polegająca na stopniowym skracaniu zadanego odcinka (patrz SectionLineSearch).
Skracanie odcinka następuje w każdej iteracji, na podstawie badania wartości funkcji w dwóch punktach: 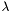 i
i 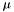 . Punkty te rozmieszczane są w taki sposób, aby dzieliły odcinek symetrycznie:
. Punkty te rozmieszczane są w taki sposób, aby dzieliły odcinek symetrycznie:
![\[ \lambda^k = a^k + (1 - \alpha) (b^k - a^k), \]](form_5.png)
![\[ \mu^k = a^k + \alpha (b^k - a^k), \]](form_6.png)
gdzie:
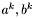 - końce zadanego odcinka,
- końce zadanego odcinka,
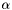 - współczynnik podziału odcinka zadany przez użytkownika,
- współczynnik podziału odcinka zadany przez użytkownika, 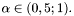
Dzięki takiemu podziałowi w każdej iteracji zachodzi:
![\[ \lambda^k - a^k = b^k - \mu^k = (1 - \alpha) (b^k - a^k) . \]](form_10.png)
Redukcja odcinka polega na odrzuceniu jednego z jego skrajnych fragmentów: ![$[a^k, \lambda^k]$](form_11.png) lub
lub ![$[\mu^k, b^k]$](form_12.png) , w zależności od wartości funkcji w punktach próbnych. W każdej iteracji odcinek jest więc skracany o długość:
, w zależności od wartości funkcji w punktach próbnych. W każdej iteracji odcinek jest więc skracany o długość:
![\[ (1 - \alpha) (b^k - a^k) .\]](form_13.png)
W przypadku gdy metoda działa samodzielnie, wynikiem jest odcinek ![$[a^k, b^k]$](form_14.png) ; jeśli służy tylko do minimalizacji kierunkowej przy rozwiązywaniu problemu optymalizacji funkcji wielu zmiennych, wynikiem jest punkt - środek tego odcinka:
; jeśli służy tylko do minimalizacji kierunkowej przy rozwiązywaniu problemu optymalizacji funkcji wielu zmiennych, wynikiem jest punkt - środek tego odcinka: 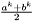 .
.
Informacje wejściowe:
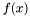 - minimalizowana funkcja jednej zmiennej,
- minimalizowana funkcja jednej zmiennej,
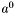 - lewy kraniec początkowego przedziału poszukiwań,
- lewy kraniec początkowego przedziału poszukiwań,
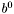 - prawy kraniec początkowego przedziału poszukiwań,
- prawy kraniec początkowego przedziału poszukiwań,
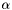 - współczynnik podziału odcinka,
- współczynnik podziału odcinka, 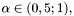
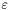 - wymagana dokładność (graniczna długość odcinka).
- wymagana dokładność (graniczna długość odcinka).
Oznaczenia:
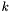 - numer aktualnej iteracji,
- numer aktualnej iteracji,
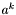 - lewy kraniec aktualnego przedziału poszukiwań,
- lewy kraniec aktualnego przedziału poszukiwań,
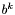 - prawy kraniec aktualnego przedziału poszukiwań,
- prawy kraniec aktualnego przedziału poszukiwań,
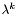 - punkt próbny znajdujący się po lewej stronie,
- punkt próbny znajdujący się po lewej stronie,
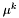 - punkt próbny znajdujący się po prawej stronie,
- punkt próbny znajdujący się po prawej stronie,
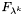 - wartość funkcji w punkcie
- wartość funkcji w punkcie 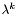 ,
,
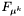 - wartość funkcji w punkcie
- wartość funkcji w punkcie 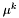 .
.
Procedura.
Krok wstępny:
Podstawiamy:
![\[ a^1 = a^0, \]](form_28.png)
![\[ b^1 = b^0, \]](form_29.png)
![\[ \lambda^1 = a^1 + (1 - \alpha) (b^1 - a^1), \]](form_30.png)
![\[ \mu^1 = a^1 + \alpha (b^1 - a^1), \]](form_31.png)
![\[ F_{\lambda^1} = f(\lambda^1), \]](form_32.png)
![\[ F_{\mu^1} = f(\mu^1), \]](form_33.png)
![\[ k = 1 . \]](form_34.png)
Krok 1:
Jeśli 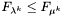 , to przechodzimy do kroku 2. W przeciwnym razie przechodzimy do kroku 3.
, to przechodzimy do kroku 2. W przeciwnym razie przechodzimy do kroku 3.
Krok 2:
Redukujemy odcinek do ![$[a^k, \mu^k]$](form_36.png) :
:
![\[ a^{k+1} = a^k, \]](form_37.png)
![\[ b^{k+1} = \mu^k \]](form_38.png)
i dokonujemy podziału otrzymanego odcinka:
![\[ \lambda^{k+1} = a^{k+1} + (1 - \alpha) (b^{k+1} - a^{k+1}), \]](form_39.png)
![\[ \mu^{k+1} = a^{k+1} + \alpha (b^{k+1} - a^{k+1}) , \]](form_40.png)
![\[ F_{\lambda^{k+1}} = f(\lambda^{k+1}), \]](form_41.png)
![\[ F_{\mu^{k+1}} = f(\mu^{k+1}). \]](form_42.png)
Przechodzimy do kroku 4.
Krok 3:
Redukujemy odcinek do ![$[\lambda^k, b^k]$](form_43.png) :
:
![\[ a^{k+1} = \lambda^k, \]](form_44.png)
![\[ b^{k+1} = b^k \]](form_45.png)
i dokonujemy podziału otrzymanego odcinka:
![\[ \lambda^{k+1} = a^{k+1} + (1 - \alpha) (b^{k+1} - a^{k+1}), \]](form_39.png)
![\[ \mu^{k+1} = a^{k+1} + \alpha (b^{k+1} - a^{k+1}) , \]](form_40.png)
![\[ F_{\lambda^{k+1}} = f(\lambda^{k+1}), \]](form_41.png)
![\[ F_{\mu^{k+1}} = f(\mu^{k+1}). \]](form_42.png)
Przechodzimy do kroku 4.
Krok 4:
Sprawdzamy warunek stopu:
Jeśli 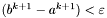 , to STOP. W przeciwnym razie podstawiamy
, to STOP. W przeciwnym razie podstawiamy 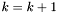 i przechodzimy do kroku 1.
i przechodzimy do kroku 1.
Szczególnym, najczęściej stosowanym przypadkiem metody jest algorytm z parametrem 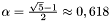 . Dla tej wartości parametru odcinek
. Dla tej wartości parametru odcinek ![$[a, b]$](form_49.png) jest w każdej iteracji dzielony przez punkty próbne na pododcinki spełniające warunek "złotego podziału":
jest w każdej iteracji dzielony przez punkty próbne na pododcinki spełniające warunek "złotego podziału":
![\[ \frac{\mu^k - a^k}{b^k - a^k} = \frac{b^k - \mu^k}{\mu^k - a^k} = \alpha, \]](form_50.png)
![\[ \frac{b^k - \lambda^k}{b^k - a^k} = \frac{\lambda^k - a^k} {b^k - \lambda^k} = \alpha, \]](form_51.png)
Stąd:
![\[ \frac{\lambda^k - a^k}{\mu^k - a^k} = \alpha . \]](form_52.png)
Dzięki ostatniej własności procedura podziałów odcinka upraszcza się: w każdej iteracji wyznaczamy tylko jeden nowy punkt próbny i, co za tym idzie, tylko raz obliczamy wartość funkcji.
Procedura.
Krok wstępny:
Podstawiamy:
![\[ a^1 = a^0, \]](form_28.png)
![\[ b^1 = b^0, \]](form_29.png)
![\[ \lambda^1 = a^1 + (1 - \alpha) (b^1 - a^1), \]](form_30.png)
![\[ \mu^1 = a^1 + \alpha (b^1 - a^1), \]](form_31.png)
![\[ F_{\lambda^1} = f(\lambda^1), \]](form_32.png)
![\[ F_{\mu^1} = f(\mu^1), \]](form_33.png)
![\[ k = 1 . \]](form_34.png)
Krok 1:
Jeśli 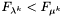 , to przechodzimy do kroku 2. W przeciwnym razie przechodzimy do kroku 3.
, to przechodzimy do kroku 2. W przeciwnym razie przechodzimy do kroku 3.
Krok 2:
Redukujemy odcinek do ![$[a^k, \mu^k]$](form_36.png) :
:
![\[ a^{k+1} = a^k, \]](form_37.png)
![\[ b^{k+1} = \mu^k \]](form_38.png)
i dokonujemy podziału otrzymanego odcinka:
![\[ \lambda^{k+1} = a^{k+1} + (1 - \alpha) (b^{k+1} - a^{k+1}), \]](form_39.png)
![\[ \mu^{k+1} = \lambda^k, \]](form_54.png)
![\[ F_{\lambda^{k+1}} = f(\lambda^{k+1}), \]](form_41.png)
![\[ F_{\mu^{k+1}} = F_{\lambda^k}. \]](form_55.png)
Przechodzimy do kroku 4.
Krok 3:
Redukujemy odcinek do ![$[\lambda^k, b^k]$](form_43.png) :
:
![\[ a^{k+1} = \lambda^k, \]](form_44.png)
![\[ b^{k+1} = b^k \]](form_45.png)
i dokonujemy podziału otrzymanego odcinka:
![\[ \lambda^{k+1} = \mu^k, \]](form_56.png)
![\[ \mu^{k+1} = a^{k+1} + \alpha (b^{k+1} - a^{k+1}) , \]](form_40.png)
![\[ F_{\lambda^{k+1}} = F_{\mu^k}, \]](form_57.png)
![\[ F_{\mu^{k+1}} = f(\mu^{k+1}). \]](form_42.png)
Przechodzimy do kroku 4.
Krok 4:
Sprawdzamy warunek stopu:
Jeśli 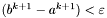 , to STOP. W przeciwnym razie podstawiamy
, to STOP. W przeciwnym razie podstawiamy 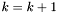 i przechodzimy do kroku 1.
i przechodzimy do kroku 1.
Taki wariant metody nazywany jest popularnie metodą złotego podziału.