#include <DichotomousDivision.h>
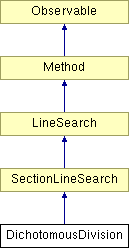
Diagram dziedziczenia dla DichotomousDivision

Metoda optymalizacji w kierunku, w której w każdym kroku zmniejszamy przedział nieoznaczoności o połowę.
Algorytm metody:
Oznaczenia:
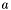 - lewy kraniec przedziału poszukiwań w danej iteracji
- lewy kraniec przedziału poszukiwań w danej iteracji
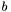 - prawy kraniec przedziału poszukiwań w danej iteracji
- prawy kraniec przedziału poszukiwań w danej iteracji
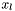 - punkt w 1/4 przedziału nieoznaczoności w danej iteracji
- punkt w 1/4 przedziału nieoznaczoności w danej iteracji
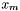 - punkt w 1/2 przedziału nieoznaczoności w danej iteracji
- punkt w 1/2 przedziału nieoznaczoności w danej iteracji
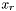 - punkt w 3/4 przedziału nieoznaczoności w danej iteracji
- punkt w 3/4 przedziału nieoznaczoności w danej iteracji
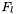 - wartość funkcji celu w punkcie
- wartość funkcji celu w punkcie 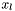
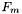 - wartość funkcji celu w punkcie
- wartość funkcji celu w punkcie 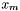
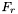 - wartość funkcji celu w punkcie
- wartość funkcji celu w punkcie 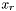
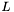 - długość odcinka nieoznaczoności
- długość odcinka nieoznaczoności
Dane potrzebne do obliczeń:
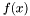 - minimalizowana funkcja jednej zmiennej
- minimalizowana funkcja jednej zmiennej
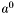 - lewy kraniec początkowego przedziału poszukiwań
- lewy kraniec początkowego przedziału poszukiwań
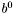 - prawy kraniec początkowego przedziału poszukiwań
- prawy kraniec początkowego przedziału poszukiwań
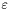 - wymagana dokładność rozwiązania
- wymagana dokładność rozwiązania
W metodzie podziału dychotomicznego dokładność rozumiana jest jako szerokość ostatniego przedziału nieokreśloności. Wymagamy by była ona mniejsza od 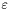 .
.
Krok 1:
Podstawić 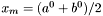 i obliczyć wartość funkcji w tym punkcie. Obliczyć
i obliczyć wartość funkcji w tym punkcie. Obliczyć 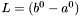 .
.
Krok 2:
Podstawić 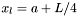 i
i 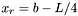 i obliczyć wartość funkcji w tych punktach.
i obliczyć wartość funkcji w tych punktach.
Krok 3:
Jeśli 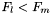 , to:
, to:
![\[ \left\{ \begin{array}{lll} b = x_m \\ x_m = x_l \\ F_m = F_l \end{array} \right. \]](form_152.png)
oraz przejść do kroku 6. Jeśli warunek nie jest spełniony, przejść do kroku 4.
Krok 4:
Jeśli 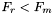 , to:
, to:
![\[ \left\{ \begin{array}{lll} a = x_m \\ x_m = x_r \\ F_m = F_r \end{array} \right. \]](form_154.png)
i przejść do kroku 6. Jeśli warunek nie jest spełniony, przejść do kroku 5.
Krok 5:
![\[ \left\{ \begin{array}{ll} a = x_l \\ b = x_r \\ \end{array} \right. \]](form_155.png)
Krok 6:
![\[ L = (b-a) \]](form_156.png)
jeśli warunek 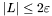 jest spełniony, zakończyć działanie algorytmu. W przeciwnym wypadku przejść do kroku 2.
jest spełniony, zakończyć działanie algorytmu. W przeciwnym wypadku przejść do kroku 2.
Algorytm zaimplementowano na podstawie:
Ostanin. A: Metody i algorytmy optymalizacji, Wydawnictwo Politechniki Białostockiej, Białystok, 2003