#include <FibonacciDivision.h>
Diagram dziedziczenia dla FibonacciDivision

Metoda Fibonacciego, opublikowana w 1953 roku przez Kiefera, jest szczególnie przydatna w sytuacjach gdy liczba obliczeń, które możemy wykonać jest ograniczona (np. w systemach czasu rzeczywistego). Metoda daje najmniejszy przedział nieokreśloności przy zadanej z góry liczbie wyliczeń funkcji.
Algorytm metody:
Oznaczenia:
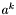 - lewy kraniec przedziału poszukiwań w k-tej iteracji
- lewy kraniec przedziału poszukiwań w k-tej iteracji
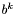 - prawy kraniec przedziału poszukiwań w k-tej iteracji
- prawy kraniec przedziału poszukiwań w k-tej iteracji
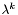 - pierwszy punkt wyliczany w k-tej iteracji
- pierwszy punkt wyliczany w k-tej iteracji
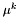 - drugi punkt wyliczany w k-tej iteracji
- drugi punkt wyliczany w k-tej iteracji
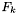 - k-ty element ciągu Fibonacciego
- k-ty element ciągu Fibonacciego
Dane potrzebne do obliczeń:
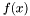 - minimalizowana funkcja jednej zmiennej
- minimalizowana funkcja jednej zmiennej
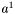 - lewy kraniec przedziału poszukiwań
- lewy kraniec przedziału poszukiwań
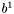 - prawy kraniec przedziału poszukiwań
- prawy kraniec przedziału poszukiwań
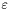 - wymagana dokładność rozwiązania
- wymagana dokładność rozwiązania
W metodzie Fibonacciego dokładność rozumiana jest jako szerokość ostatniego przdziału nieokreśloności. Wymagamy by była ona mniejsza od 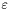 . Charakterystyczną cechą metody Fibonacciego jest to, że liczbę kroków optymalizacji ustalamy przed rozpoczęciem obliczeń.
. Charakterystyczną cechą metody Fibonacciego jest to, że liczbę kroków optymalizacji ustalamy przed rozpoczęciem obliczeń. 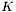 musi spełniać warunek:
musi spełniać warunek: 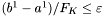 .
.
Krok 1:
Tworzymy dwa nowe punkty (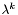 i
i 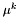 ) leżące pomiędzy
) leżące pomiędzy a i b zgodnie ze wzorami:
![\[ \lambda^k = a^k + \frac{F_{K-k-1}}{F_{K-k+1}}(b^k - a^k) \]](form_174.png)
![\[ \mu^k = a^k + \frac{F_{K-k}}{F_{K-k+1}}(b^k - a^k) \]](form_175.png)
W nowoutworzonych punktach wyliczamy wartość funkcji.
Krok 2:
Jeśli 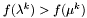 , to podstawiamy:
, to podstawiamy:
![\[ \left\{ \begin{array}{llll} a^{k+1} = \lambda^k \\ b_{k+1} = b^k \\ \lambda^{k+1} = \mu^k \\ \mu^{k+1} = a^{k+1} + \frac{F_{K-i}}{F_{K-k+1}}(b^{k+1} - a^{k+1}) \end{array} \right. \]](form_177.png)
oraz obliczamy wartość funkcji w punkcie 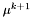 . Następnie przechodzimy do punktu 4.
. Następnie przechodzimy do punktu 4.
Jednak gdy 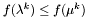 przechodzimy do kroku 3.
przechodzimy do kroku 3.
Krok 3:
Podstawiamy
![\[ \left\{ \begin{array}{llll} a^{k+1} = a^k \\ b^{k+1} = \mu^k \\ \mu^{k+1} = \lambda^k \\ \lambda^{k+1} = a^{k+1} + \frac{F_{K-k-1}}{F_{K-k+1}}(b^{k+1} - a^{k+1}) \end{array} \right. \]](form_180.png)
i wyliczamy wartość funkcji w punkcie 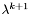 . Następnie przechdzimy do punktu 4.
. Następnie przechdzimy do punktu 4.
Krok 4:
Podstawiamy 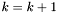 . Jeśli
. Jeśli 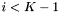 , to przejść do kroku 2. W przeciwnym wypadku przejść do kroku 5.
, to przejść do kroku 2. W przeciwnym wypadku przejść do kroku 5.
Krok 5:
![\[ \left\{ \begin{array}{ll} \lambda^K = \lambda^{K-1} \\ \mu^K = \lambda^K + \varepsilon \end{array} \right. \]](form_183.png)
Jeśli 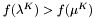 , to podstawiamy:
, to podstawiamy:
![\[ \left\{ \begin{array}{ll} a^K = \lambda^K \\ b^K = b^{K-1} \end{array} \right. \]](form_185.png)
Jeśli natomiast 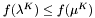 , to podstawiamy:
, to podstawiamy:
![\[ \left\{ \begin{array}{ll} a^K = a^{K-1} \\ b^K = \lambda^K \end{array} \right. \]](form_187.png)
Wynikiem działania metody jest punkt w środku odcinka ![$ [a, b] $](form_188.png) .
.