Dokumentacja klasy FletcherReeves

#include <FletcherReeves.h>

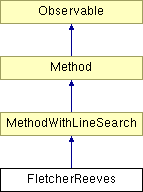
Diagram dziedziczenia dla FletcherReeves

Opis szczegółowy

Metoda Fletchera-Reevesa.

Matoda Fletchera-Reevesa należy do klasy metod gradientów sprzężonych, co oznacza, że do otrzymywania kierunków sprzężonych wykorzystano w niej wartości składników gradientów.

Metoda powinna znaleźć minimum dowolnej funkcji kwadratowej w liczbie kroków co najwyżej równej wymiarowi problemu.

Algorytm metody:

Oznaczenia:
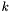$ k $ - numer aktualnej iteracji
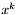$x^k$ - punkt w 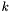$k$ -tej iteracji,
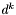$d^k$ - kierunek poszukiwań w 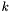$k$ -tej iteracji,
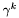$\gamma^k$ -współczynnik zapewniający sprzężenie nowego kierunku 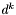$d^k$ z poprzednim,
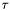$\tau$ - długość kroku

Dane potrzebne do obliczeń:
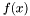$ f(x) $ - minimalizowana funkcja celu
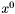$ x^0 $ - punkt startowy
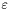$\varepsilon$ - wymagana dokładność
warunek stopu - do wyboru:

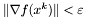
$\|\nabla f(x^k)\| < \varepsilon$
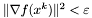
$\|\nabla f(x^k)\|^2 < \varepsilon$
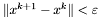$\|x^{k+1} - x^k\| < \varepsilon$ ,
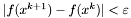$|f(x^{k+1}) - f(x^k)| < \varepsilon$ ,
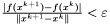$\frac{|f(x^{k+1}) - f(x^k)|}{\|x^{k+1} - x^k\|} < \varepsilon$ .

Krok 0 (wstępny):
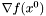Oblicz $\nabla f(x^0)$ .
Podstaw $ k=0 $

.
Przejdź do kroku 1.

Krok 1:
Jeśli spełniony jest warunek stopu, to przerwij działanie algorytmu i jako wynik przedstaw $ x^k $

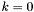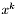. W przeciwnym wypadku przejdź do kroku 2.

Krok 2:
Przejdź do kroku 3, jeśli $ k=0 $

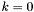gdy używana jest tradycyjna wersja algorytmu lub jeśli 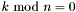$k \mbox{ mod } n = 0$ w przypadku gdy wprowadzono modyfikację (patrz: Uwagi). W przeciwnym wypadku przejdź do kroku 4.

Krok 3:
Podstaw:

$d^k = -\nabla(f(x^k))$

Przejdź do kroku 5.

Krok 4:
Podstaw:

$d^k = -\nabla(f(x^k)) + \gamma^{k-1} d^{k-1}$

gdzie:

$\gamma^k = \frac{\|\nabla f(x^k)\|^2}{\|\nabla f(x^{k-1}))\|^2}$

Przejdź do kroku 5.
Krok 5:

$x^{k+1} = x^k + \tau d^k ,$

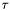gdzie $\tau$ dobierane jest tak, by funkcja 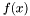$ f(x) $ osiągała minimum w kierunku $ d^k $ .
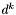Podstaw: 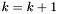$ k = k+1 $ .
Przejdź do kroku 1.

Uwagi:

Modyfikacja wprowadzona do oryginalnego algorytmu Fletchera-Reevesa polega na powracaniu do poszukiwań w kierunku przeciwnym do gradientu po wykonaniu liczby kroków równej wymiarowi problemu. Pozwala on na zapobieżenie wygenerowaniu kierunków liniowo zależnych, co powoduje spowolnienie zbieżności.

Algorytm zaimplementowano na podstawie:
Ostanin. A: Metody i algorytmy optymalizacji, Wydawnictwo Politechniki Białostockiej, Białystok, 2003

Niniejszy dokument został półautomatycznie wycięty z dokumentacji kodu źródłowego programu Eduoptim 2. Pełna dokumentacja dostępna jest wraz ze źródłami bądź osobno w dziale pliki.
Hierarchia klas w programie nie odpowiada klasyfikacji metod optymalizacji.