Dokumentacja klasy Marquardt

#include <Marquardt.h>

Diagram dziedziczenia dla Marquardt

Opis szczegółowy

Metoda Marquardta.

Metoda Marquardta jest udaną próbą połączenia korzystnych właściwości metod największego spadku i Newtona. Metoda Newtona zbiega się szybko w pobliżu minimum, natomiast metoda Cauchy'ego w dużym od niego oddaleniu.

Algorytm metody:

Oznaczenia:
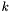$ k $ - numer aktualnej iteracji
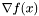$\nabla f(x)$ - gradient w punkcie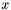 $ x $
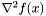$\nabla^2 f(x)$ - macierz hesjanu w punkcie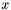 $ x $
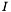$ I $ - macierz jednostkowa
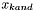$x_{kand}$ - kandydat na punkt w następnej iteracji (odrzucany po kroku próbnym gdy nie nastąpiło zmniejszenie wartości funkcji celu)

Dane potrzebne do obliczeń:
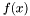$ f(x) $ - minimalizowana funkcja celu
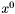$ x^0 $ - punkt startowy
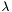$\lambda$ - współczynnik wagi macierzy jednostkowej
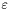$\varepsilon$ - wymagana dokładność
warunek stopu - do wyboru:

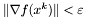
$\|\nabla f(x^k)\| < \varepsilon$
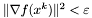
$\|\nabla f(x^k)\|^2 < \varepsilon$
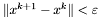$\|x^{k+1} - x^k\| < \varepsilon$ ,
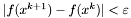$|f(x^{k+1}) - f(x^k)| < \varepsilon$ ,
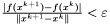$\frac{|f(x^{k+1}) - f(x^k)|}{\|x^{k+1} - x^k\|} < \varepsilon$ .

Krok 0 (wstępny):
Podstaw $ k=0 $

.
Wylicz wartości funkcji, gradientu i macierzy hesjanu w punkcie $ x^0 $

.

Krok 1:
Sprawdź czy spełniony jest warunek stopu. Jeśli tak, to przerwij działanie algorytmu i przedstaw $ x^k $

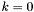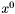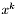jako wynik. W przeciwnym wypadku przejdź do kroku 2.

Krok 2:
Oblicz:

$x_{kand} = x^k + \tau^k$

gdzie:

$\tau^k = -[\nabla^2 f(x^k) + \lambda I]^{-1} \nabla f(x^k)$

Krok 3:
Jeśli 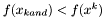$f(x_{kand}) < f(x^k)$ , to przejdź do kroku 4. W przeciwnym wypadku przejdź do kroku 5.

Krok 4:
Podstaw:

$\lambda = \frac{1}{2} \lambda$

$x^{k+1} = x_{kand}$

$k=k+1$

, a następnie przejdź do kroku 1.

Krok 5:
Podstaw 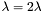$\lambda = 2 \lambda$ i przejdź do kroku 2.

Uwagi:
W algorytmnie nie ma minimalizacji w kierunku, gdyż długość kroku reguluje już współczynnik 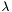$\lambda$ . Na początku działania algorytmu wartość współczynnika 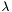$\lambda$ musi być bardzo duża aby wartości na przekątnej macierzy jednostkowej miały większe znaczenie dla sumy we wzorze na kierunek. Z każdym udanym krokiem (tzn. takim, dla którego wartość funkcji w x maleje) lambda zmniejsza się o połowę aż do momentu, w którym to wartości hesjanu stają się ważniejsze dla wyznaczania kierunku. Podobnie jak w innych metodach, na początku działania algorytmu zmienne określające odległość dwóch ostatnich punktów i różnicę wartości funkcji w tych punktach mają wartości DBL_MAX. Wynika z tego, że algorytm może się zatrzymać bez wykonania żadnej iteracji jedynie w przypadku użycia kryterium "gradientowego". Jest to zachowanie jak najbardziej pożądane.

Algorytm zaimplementowano na podstawie:
Ostanin. A: Metody i algorytmy optymalizacji, Wydawnictwo Politechniki Białostockiej, Białystok, 2003<>

Niniejszy dokument został półautomatycznie wycięty z dokumentacji kodu źródłowego programu Eduoptim 2. Pełna dokumentacja dostępna jest wraz ze źródłami bądź osobno w dziale pliki.
Hierarchia klas w programie nie odpowiada klasyfikacji metod optymalizacji.