#include <NelderMead.h>
Diagram dziedziczenia dla NelderMead

W metodzie Neldera-Meada po wykresie funkcji pełza sympleks złożony z N+1 punktów, gdzie N oznacza liczbę wymiarów problemu.
Algorytm metody:
Oznaczenia:
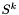 - zbiór punktów sympleksu w k-tej iteracji
- zbiór punktów sympleksu w k-tej iteracji
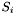 - zbiór indeksów punktów należących do
- zbiór indeksów punktów należących do 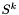 .
.
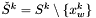
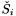 - zbiór indeksów punktów należących do
- zbiór indeksów punktów należących do 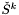
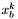 - najlepszy punkt sympleksu w k-tej iteracji
- najlepszy punkt sympleksu w k-tej iteracji
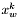 - najgorszy punkt sympleksu w k-tej iteracji
- najgorszy punkt sympleksu w k-tej iteracji
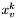 - prawie najgorszy punkt sympleksu w k-tej iteracji
- prawie najgorszy punkt sympleksu w k-tej iteracji
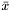 - środek ciężkości zbioru
- środek ciężkości zbioru 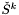
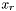 - punkt powstały poprzez odbicie najgorszego punktu sympleksu względem punktu
- punkt powstały poprzez odbicie najgorszego punktu sympleksu względem punktu 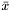
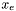 - punkt przesunięty jeszcze dalej w tym samym kierunku, w którym nastąpiło odbicie najgorszego punktu sympleksu przy tworzeniu punktu
- punkt przesunięty jeszcze dalej w tym samym kierunku, w którym nastąpiło odbicie najgorszego punktu sympleksu przy tworzeniu punktu 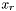
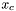 - punkt znajdujący się pomiędzy najgorszym punktem sympleksu, a środkiem ciężkości pozostałych jego punktów lub tymże środkiem ciężkości, a punktem
- punkt znajdujący się pomiędzy najgorszym punktem sympleksu, a środkiem ciężkości pozostałych jego punktów lub tymże środkiem ciężkości, a punktem 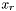
Dane potrzebne do obliczeń:
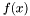 - funkcja celu
- funkcja celu
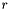 - współczynnik odbicia (
- współczynnik odbicia (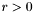 , domyślnie 1)
, domyślnie 1)
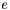 - współczynnik rozciągnięcia (
- współczynnik rozciągnięcia (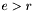 , domyślnie 2)
, domyślnie 2)
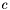 - współczynnik ściśnięcia (
- współczynnik ściśnięcia (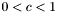 , domyślnie
, domyślnie 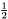 )
)
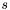 - współczynnik skurczenia (
- współczynnik skurczenia (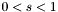 , domyślnie
, domyślnie 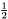 )
)
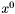 - środek początkowego sympleksu
- środek początkowego sympleksu
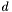 - długość krawędzi początkowego sympleksu
- długość krawędzi początkowego sympleksu
Krok 0 (wstępny):
W tym kroku wyliczamy współrzędne wierzchołków początkowego sympleksu w ten sposób, by punkt 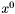 znalazł się w jego środku.
znalazł się w jego środku.
Poniższe wzory potrzebne do utworzenia regularnego sympleksu zaczerpnięto z [1].
Wzór na wyliczenie j-tej współrzędnej i-tego wierzchołka sympleksu ma postać:
![\[ x^{(j)}_i = \left\{ \begin{array}{ll} x^{(j)}_0 + \delta_1 \mbox{ gdy } i \not= j;\\ x^{(j)}_0 + \delta_2 \mbox{ gdy } i = j. \end{array} \right. \]](form_277.png)
Wartości współczynnika 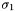 i
i 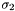 wyliczamy ze wzorów:
wyliczamy ze wzorów:
![\[ \delta_1 = \left(\frac{\sqrt{N+1}+N-1}{N\sqrt{2}}\right)\frac{d}{2} \]](form_280.png)
![\[ \delta_2 = \left(\frac{\sqrt{N+1}-1}{N\sqrt{2}}\right)\frac{d}{2} \]](form_281.png)
W powyższy sposób otwrzymujemy zbiór 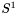 .
.
W wierzchołkach aktualnego sympleksu wyliczamy wartości funkcji.
Wybieramy szczególne punkty sympleksu: 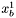 ,
, 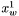 i
i 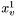 . Zapamiętujemy rownież wartości funkcji
. Zapamiętujemy rownież wartości funkcji 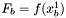 ,
, 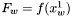 oraz
oraz 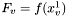
Podstawiamy 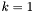 i przechodzimy do kroku 1.
i przechodzimy do kroku 1.
Krok 1:
Wyliczamy środek ciężkości punktów sympleksu z pominięciem punktu najgorszego wg wzoru:
![\[ \bar{x} = \frac{ \sum_{i \in \check{S}_i} x_i }{N} \]](form_290.png)
Przechodzimy do kroku 2.
Krok 2:
Wyznaczamy punkt 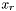 poprzez odbicie najgorszego punktu sympleksu względem środka ciężkości:
poprzez odbicie najgorszego punktu sympleksu względem środka ciężkości:
![\[ x_r = \bar{x} + r(\bar{x}-x^k_w) \]](form_291.png)
Wyliczamy wartość funkcji celu w tym punkcie.
Jeśli 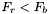 , to przechodzimy do kroku 3. W przeciwnym przypadku przechodzimy do kroku 5.
, to przechodzimy do kroku 3. W przeciwnym przypadku przechodzimy do kroku 5.
Krok 3:
Wyznaczamy punkt 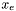 zgodnie ze wzorem:
zgodnie ze wzorem:
![\[ x_e = \bar{x} + e(\bar{x}-x^k_w) \]](form_293.png)
Wyliczamy wartość funkcji w tym punkcie.
Jeśli 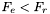 to przechodzimy do kroku 4a. W przeciwnym wypadku przechodzimy do kroku 4b.
to przechodzimy do kroku 4a. W przeciwnym wypadku przechodzimy do kroku 4b.
Krok 4a:
W sympleksie zastępujemy punkt 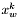 punktem
punktem 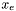 i przechodzimy do kroku 12.
i przechodzimy do kroku 12.
Krok 4b:
W sympleksie zastępujemy punkt 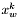 punktem
punktem 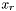 i przechodzimy do kroku 12.
i przechodzimy do kroku 12.
Krok 5:
Jeśli 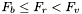 , to przechodzimy do kroku 6. W przeciwnym wypadku przechodzimy do kroku 7.
, to przechodzimy do kroku 6. W przeciwnym wypadku przechodzimy do kroku 7.
Krok 6:
W sympleksie zastępujemy punkt 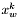 punktem
punktem 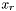 i przechodzimy do kroku 12.
i przechodzimy do kroku 12.
Krok 7:
Jeśli 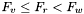 , to przechodzimy do kroku 8. W przeciwnym Wypadku przechodzimy do kroku 9.
, to przechodzimy do kroku 8. W przeciwnym Wypadku przechodzimy do kroku 9.
Krok 8:
Wyznaczamy punkt 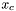 ze wzoru:
ze wzoru:
![\[ x_c = x_r - c(x_r - \bar{x}) \]](form_297.png)
Wyliczamy w tym punkcie wartość funkcji.
Jeśli 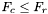 , przechodzimy do kroku 10. W przeciwnym wypadku przechodzimy do kroku 11.
, przechodzimy do kroku 10. W przeciwnym wypadku przechodzimy do kroku 11.
Krok 9:
Wyznaczamy punkt 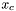 ze wzoru:
ze wzoru:
![\[ x_c = x^k_w + c(\bar{x} - x^k_w) \]](form_299.png)
Wyliczamy w tym punkcie wartość funkcji.
Jeśli 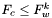 , przechodzimy do kroku 10. W przeciwnym wypadku przechodzimy do kroku 11.
, przechodzimy do kroku 10. W przeciwnym wypadku przechodzimy do kroku 11.
Krok 10:
W sympleksie zastępujemy punkt 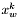 punktem
punktem 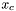 i przechodzimy do kroku 12.
i przechodzimy do kroku 12.
Krok 11:
Dokonujemy skurczenia sympleksu w kierunku punktu najlepszego zgodnie z procedurą:
![\[ x^{k+1}_i = x^k_i - s(x^k_i - x_b) \mbox{ dla } i \in S_i\]](form_301.png)
Oczywiście w wyniku działania tej procedury punkt najlepszy nie zmieni swojego położenia.
W nowych punktach obliczamy wartości funkcji.
Krok 12:
Podstawiamy 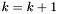 .
.
Wybieramy szczególne punkty sympleksu: 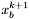 ,
, 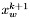 i
i 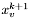 . Zapamiętujemy rownież wartości funkcji
. Zapamiętujemy rownież wartości funkcji 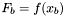 ,
, 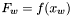 oraz
oraz 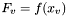
Przechodzimy do kroku 13.
Krok 13:
Jeśli spełniony jest warunek stopu, zakończ działanie algorytmu. Punktem wynikowym jest najlepszy punkt ostatniego sympleksu.
Jeśli warunek niejest spełniony przechodzimy do kroku 1.
Uwagi:
W metodzie można zastosować kilka rożnych warunków stopu
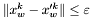 , gdzie poprzez
, gdzie poprzez 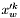 oznaczamy punkt, który zastąpił w sympleksie punkt
oznaczamy punkt, który zastąpił w sympleksie punkt 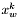 . Ten warunek jest odpowiednikiem tradycyjnego warunku sprawdzającego długość wykonanego kroku, wykorzystywanego często w metodach gradientowych.
. Ten warunek jest odpowiednikiem tradycyjnego warunku sprawdzającego długość wykonanego kroku, wykorzystywanego często w metodach gradientowych. 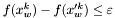 , gdzie poprzez
, gdzie poprzez 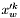 oznaczamy punkt, który zastąpił w sympleksie punkt
oznaczamy punkt, który zastąpił w sympleksie punkt 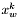 .
. 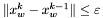 .
. 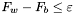 .
. 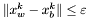 .
. 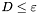 , gdzie
, gdzie 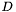 oznacza sumę długości wszystkich krawędzi sympleksu.
oznacza sumę długości wszystkich krawędzi sympleksu. [1] Aleksander Ostanin - Metody i algorytmy optymalizacji, Wydawnictwo Politechniki Białostockiej, Białystok 2003 oraz: [2] J. C. Lagarias, J. A. Reeds, M. H. Wright, P. E. Wright - Convergence Properties of the Nelder-Mead Simplex Function in low dimensions. (SIAM Journal on Optimization, Vol. 1, No. 1, pp 112-147).
W drugim źródle zaproponowano sposoby postępowania w przypadku gdy co najmniej w dwóch wierzchołkach sympleksu wartość funkcji jest taka sama.