Dokumentacja klasy NewtonRaphson

#include <NewtonRaphson.h>

Diagram dziedziczenia dla NewtonRaphson

SinglePointLineSearch LineSearch Method Observable Lista wszystkich składowych.

Opis szczegółowy

Metoda Newtona-Raphsona.

Metoda Newtona-Raphsona jest oparta na kwadratowym modelu funkcji - rozwinięciu funkcji celu w szereg Taylora drugiego rzędu. Dla funkcji jednej zmiennej takie rozwinięcie (z pominięciem reszty Lagrange'a) ma postać:

\[ q(x) = f(x_k) + f'(x_k)(x - x_k) + \frac{1}{2} f''(x_k)(x - x_k)^2 . \]

Chcąc znaleźć ekstremum powyższej funkcji, należy (z warunku koniecznego na istnienie ekstremum) wyzerować jej pochodną, która jest następująca:

\[ q'(x) = f'(x_k) + f''(x_k)(x - x_k) . \]

Stąd bierze się wzór na kolejne punkty w metodzie Newtona-Raphsona:

\[ x^k = x^{k-1}-\frac{f'(x^{k-1})}{f''(x^{k-1})} . \]

W powyższy sposób metoda znajduje minimum funkcji kwadratowej w zaledwie jednej iteracji. Minimalizacja funkcji wyższego rzędu niż kwadratowa (czyli wyższego rzędu niż zastosowany model) może zająć więcej iteracji.
Należy zauważyć, że powyższa metoda pozwala znaleźć ekstremum, niekoniecznie minimum. Z tego powodu w implementacji algorytmu dodano sprawdzanie znaku drugiej pochodnej - jeżeli jest ona ujemna, metoda kończy działanie.
Ponadto, taka metoda wyznaczania kolejnych punktów wymaga oczywiście, aby funkcja celu była podwójnie różniczkowalna.

Warunek stopu metody jest oparty na szacowanej odległości do ekstremum:

\[ |f'(x)| < \varepsilon . \]

Algorytm metody:

Oznaczenia:
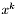$ x^k $ - punkt w k-tej iteracji

Dane potrzebne do obliczeń:
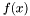$ f(x) $ - minimalizowana funkcja jednej zmiennej
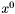$ x^0 $ - punkt początkowy
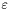$ \varepsilon $ - wymagana dokładność rozwiązania

Krok wstępny:
Podstaw:

\[ x^1 = x^0, \]

\[ k = 1. \]

Krok 1:
Oblicz 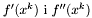$f'(x^k)$ i $f''(x^k)$.
Przejdź do kroku 2.

Krok 2:
Sprawdź warunek stopu.
Jeśli jest on spełniony, to STOP. Wynikiem jest 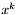$x^k$.
W przeciwnym wypadku przejdź do kroku 3.

Krok 3:
Sprawdź wartość drugiej pochodnej w punkcie 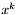$x^k$:
jeśli 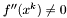$f''(x^k) \neq 0$, to przejdź do kroku 4.
W przeciwnym wypadku STOP - druga pochodna równa zeru, optymalizacji nie można kontynuować.

Krok 4:
Podstaw 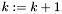$k := k+1$.
Wyznacz kolejny punkt:

\[ x^k = x^{k-1} - \frac{f'(x^{k-1})}{f''(x^{k-1})} . \]

Przejdź do kroku~1.

Algorytm zaimplementowano na podstawie:
Ostanin. A: Metody i algorytmy optymalizacji, Wydawnictwo Politechniki Białostockiej, Białystok, 2003

Zobacz również:
Linesearch

Niniejszy dokument został półautomatycznie wycięty z dokumentacji kodu źródłowego programu Eduoptim 2. Pełna dokumentacja dostępna jest wraz ze źródłami bądź osobno w dziale pliki.
Hierarchia klas w programie nie odpowiada klasyfikacji metod optymalizacji.