Dokumentacja klasy PowellVariant2

#include <PowellVariant2.h>

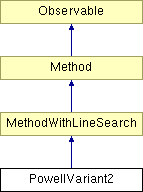
Diagram dziedziczenia dla PowellVariant2

Opis szczegółowy

Metoda Powella - wariant drugi.

Bezgradientowa metoda kierunków sprzężonych.

Od wariantu pierwszego odróżnia ją metoda modyfikacji bazy kierunków 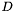$D$ (krok 4 procedury). Metoda zaimplementowana w tym wariancie gwarantuje zachowanie liniowej niezależności kierunków.

Metoda oparta na dwóch twierdzeniach:
1. Dla wzajemnie sprzężonych względem dodatnio określonej macierzy 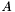$A$ kierunków

$d^{(1)}, \: d^{(2)}, \: \ldots, \: d^{(n)}$

minimum formy kwadratowej

$f(x) = q + b^T x + \frac{1}{2} x^T A x$

może być znalezione w wyniku minimalizacji funkcji 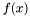$f(x)$ wzdłuż każdego z kierunków 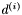$d^{(i)}$ tylko raz.
Kierunki 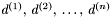$d^{(1)}, \: d^{(2)}, \: \ldots, \: d^{(n)}$ są wzajemnie sprzężone względem dodatnio określonej macierzy 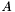$A$ , gdy spełniony jest warunek:

$(d^{(i)})^T A d^{(j)} = 0 \mbox{ dla wszystkich } i \neq j.$

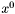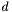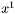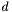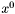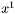2. Jeśli $x^0$ jest minimum w kierunku $d$ należącym do pewnej rozmaitości liniowej oraz jeśli $x^1$ jest minimum w tym samym kierunku $d$ , ale w innej rozmaitości zawierającej ten kierunek (np. $x^0$ i $x^1$ znaleziono w wyniku minimalizacji w kierunku 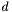$d$ zaczynając z różnych punktów startowych), to kierunek

$(x^1 - x^0)$

łączący te dwa punkty jest sprzężony z kierunkiem 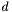$d$ .

Twierdzenie 1 zapewnia, że metoda, przy wykorzystaniu dokładnych poszukiwań w kierunku, będzie znajdować minimum wielomianu drugiego stopnia w 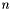$n$ krokach, gdzie 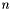$n$ jest liczbą zmiennych.
Twierdzenie 2 dostarcza łatwej metody generowania kierunków sprzężonych.

Informacje wejściowe:
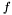$f$ - minimalizowana funkcja 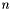$n$ zmiennych,
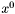$x^0$ - dowolnie wybrany punkt startowy,
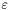$\varepsilon$ - wymagana dokładność obliczeń,
warunek stopu - do wyboru:

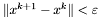$\|x^{k+1} - x^k\| < \varepsilon$ ,
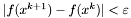$|f(x^{k+1}) - f(x^k)| < \varepsilon$ ,
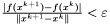$\frac{|f(x^{k+1}) - f(x^k)|}{\|x^{k+1} - x^k\|} < \varepsilon$ ,

wybrana metoda minimalizacji w kierunku wraz z parametrami.

Oznaczenia:
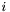$i$ - indeks aktualnego kierunku,
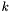$k$ - numer aktualnej iteracji,
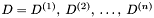$D = D^{(1)},\: D^{(2)}, \: \ldots, \: D^{(n)}$ - baza wzajemnie ortogonalnych kierunków (macierz utworzona z wektorów kolumnowych),
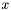$x$ - aktualny punkt,
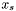$x_s$ - punkt startowy etapu,
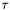$\tau$ - długość optymalnego krok w danym kierunku 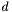$d$ , wyznaczona przez metodę optymalizacji w kierunku,
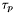$\tau_p$ - najdłuższy krok wzdłuż jednego z 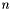$n$ kierunków w fazie przeszukiwania,
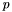$p$ - indeks kierunku, w którym wykonano najdłuższy krok,
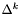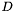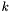$\Delta^k$ - wyznacznik macierzy kierunków $D$ w $k$ -tej iteracji,
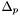$\Delta_p$ - wyznacznik macierzy kierunków 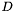$D$ po ewentualnym umieszczeniu w~niej nowego kierunku sprzężonego.

Procedura.

Krok wstępny:
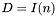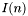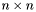Podstawiamy $ D = I(n) $ , gdzie $I(n)$ - macierz identycznościowa o wymiarach $n \times n$ .
Obliczamy pierwszy punkt początkowy:

$\tau = \arg \min_{\tau} f(x + \tau D^{(n)}),$

$x_s = x^0 + \tau D^{(n)}.$

Podstawiamy:

$x = x_s,$

$\Delta^1 = 1,$

$\tau_p = 0,$

$k = 1 ,$

$i = 1 .$

Krok 1:
Przy pomocy metody optymalizacji w kierunku wyznaczamy optymalną długość kroku 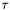$\tau$ i wykonujemy krok:

$\tau = \arg \min_{\tau} f(x + \tau D^{(i)}) .$

$x = x + \tau D^{(i)} .$

Jeśli wykonany krok jest najdłuższy w etapie (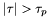 $|\tau| > \tau_p$ ), to zapamiętujemy jego długość i indeks kierunku:

$\tau_p = |\tau|,$

$p = i.$

Podstawiamy 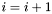$i = i + 1$ i sprawdzamy, czy 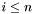$i \le n$ . Jeśli tak, ponownie wykonujemy krok 1. Jeśli nie, podstawiamy 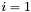$i = 1$ i przechodzimy do kroku 2.

Krok 2:
Sprawdzamy warunek stopu. Jeśli jest on spełniony, to STOP. Wynikiem jest 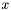$x$ .
W przeciwnym razie przechodzimy do kroku 3.

Krok 3:
Wyznaczamy nowy kierunek sprzężony:

$D^{(n+1)} = \frac{x - x_s}{\| x - x_s \|} .$

Następnie wykonujemy krok o optymalnej długości w tym kierunku:

$\tau = \arg \min_{\tau} f(x + \tau D^{(n+1)}) ,$

$x = x + \tau D^{(n+1)}.$

Krok 4:
Sprawdzamy warunek modyfikacji bazy:

$\Delta_p = \frac{\tau_p \Delta^k}{\|x - x_s\|} \ge 0,8 \; ,$

Jeśli warunek ten jest spełniony, kierunek, w którym wykonano najdłuższy krok 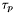$\tau_p$ , zostaje zastąpiony nowym kierunkiem sprzężonym:

$D^{(p)} = D^{(n+1)}$

i zostaje zapamiętany nowy wyznacznik bazy:

$\Delta^{k+1} = \Delta_p.$

Jeśli warunek nie jest spełniony, baza kierunków nie jest zmieniana.
Podstawiamy aktualny punkt za punkt startowy dla kolejnego etapu:

$x_s = x.$

Podstawiamy 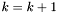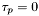$k = k + 1$ , $\tau_p = 0$ i wracamy do kroku 1.

Uwagi.
Wariant ten jest mniej wydajny od podstawowego, jednak gwarantuje zachowanie liniowej niezależności kierunków.

Metoda zaimplementowana na podstawie opisu zamieszczonego w:
Findeisen W., Szymanowski J., Wierzbicki A.: Teoria i metody obliczeniowe optymalizacji. Warszawa, PWN 1977.
W odróżnieniu od tego opisu, w implementacji warunek stopu sprawdzany jest przed obliczeniem nowego kierunku sprzężonego, w celu uniknięcia ryzyka dzielenia przez 0 przy wyznaczaniu kierunku.

Zobacz również:: MethodWithLineSearch
PowellVariant1

Niniejszy dokument został półautomatycznie wycięty z dokumentacji kodu źródłowego programu Eduoptim 2. Pełna dokumentacja dostępna jest wraz ze źródłami bądź osobno w dziale pliki.
Hierarchia klas w programie nie odpowiada klasyfikacji metod optymalizacji.