#include <QuadraticApproximation.h>
Diagram dziedziczenia dla QuadraticApproximation

Metoda optymalizacji w kierunku polegająca na stopniowym skracaniu zadanego odcinka (patrz SectionLineSearch).
Opiera się na założeniu, że w otoczeniu minimum funkcja celu może być aproksymowana funkcją kwadratową.
W każdej iteracji dokonywana jest minimalizacja funkcji kwadratowej zbudowanej na podstawie wartości funkcji celu w trzech punktach próbnych: 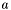 ,
, 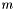 i
i 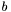 . Do skonstruowania takiej funkcji aproksymującej wykorzystywana jest interpolacja Lagrange'a:
. Do skonstruowania takiej funkcji aproksymującej wykorzystywana jest interpolacja Lagrange'a:
![\[ f(x) = F_a \frac{(x - a)(x - b)}{(a - m)(a - b)} + F_m \frac{(x - a)(x - b)}{(m - a)(m - b)} + F_b \frac{(x - a)(x - m)}{(b - a)(b - m)} . \]](form_379.png)
Pierwsza pochodna tej funkcji zeruje się w punkcie:
![\[ x = \frac{1}{2} \frac{(m^2 - b^2)F_a + (b^2 - a^2)F_m + (a^2 - m^2)F_b} {(m - b)F_a + (b - a)F_m + (a - m)F_b}.\]](form_380.png)
Algorytm polega na zastępowaniu jednego z punktów próbnych 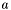 ,
, 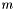 ,
, 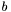 punktem
punktem 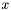 i skracaniu odcinka w taki sposób, aby obejmował on estymowane minimum.
i skracaniu odcinka w taki sposób, aby obejmował on estymowane minimum.
Informacje wejściowe:
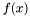 - minimalizowana funkcja jednej zmiennej,
- minimalizowana funkcja jednej zmiennej,
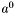 - lewy kraniec początkowego przedziału poszukiwań,
- lewy kraniec początkowego przedziału poszukiwań,
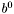 - prawy kraniec początkowego przedziału poszukiwań,
- prawy kraniec początkowego przedziału poszukiwań,
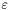 - wymagana dokładność (graniczna długość odcinka, minimalna odległość
- wymagana dokładność (graniczna długość odcinka, minimalna odległość 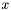 od punktów próbnych).
od punktów próbnych).
Oznaczenia:
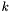 - numer aktualnej iteracji,
- numer aktualnej iteracji,
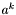 - lewy kraniec aktualnego przedziału poszukiwań - pierwszy punkt próbny,
- lewy kraniec aktualnego przedziału poszukiwań - pierwszy punkt próbny,
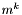 - drugi punkt próbny,
- drugi punkt próbny,
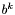 - prawy kraniec aktualnego przedziału poszukiwań - trzeci punkt próbny,
- prawy kraniec aktualnego przedziału poszukiwań - trzeci punkt próbny,
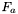 - wartość funkcji celu w punkcie
- wartość funkcji celu w punkcie 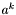 ,
,
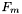 - wartość funkcji celu w punkcie
- wartość funkcji celu w punkcie 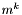 ,
,
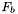 - wartość funkcji celu w punkcie
- wartość funkcji celu w punkcie 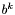 ,
,
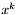 - punkt zerowania się pierwszej pochodnej funkcji aproksymującej,
- punkt zerowania się pierwszej pochodnej funkcji aproksymującej,
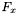 - wartość funkcji celu w punkcie
- wartość funkcji celu w punkcie 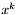 .
.
Procedura.
Krok wstępny:
Podstawiamy:
![\[ a^1 = a^0, \]](form_28.png)
![\[ m^1 = \frac{a^0 + b^0}{2}, \]](form_386.png)
![\[ b^1 = b^0, \]](form_29.png)
![\[ F_a = f(a^1), \]](form_387.png)
![\[ F_m = f(m^1), \]](form_388.png)
![\[ F_b = f(b^1). \]](form_389.png)
Krok 1:
Znajdujemy potencjalne minimum funkcji aproksymującej:
![\[ x^k = \frac{1}{2} \frac{((m^k)^2 - (b^k)^2)F_a + ((b^k)^2 - (a^k)^2)F_m + ((a^k)^2 - (m^k)^2)F_b} {(m^k - b^k)F_a + (b^k - a^k)F_m + (a^k - m^k)F_b}.\]](form_390.png)
Jeśli mianownik tego wyrażenia jest liczbą nieujemną, przechodzimy do kroku 8.
Podstawiamy 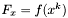 i przechodzimy do kroku 2.
i przechodzimy do kroku 2.
Krok 2:
Sprawdzamy, czy 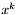 znajduje się wystarczająco blisko jednego z punktów próbnych:
znajduje się wystarczająco blisko jednego z punktów próbnych:
Jeśli 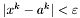 lub
lub 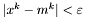 lub
lub 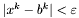 , to przechodzimy do kroku 7.
, to przechodzimy do kroku 7.
Sprawdzamy, czy 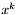 leży wewnątrz badanego odcinka:
leży wewnątrz badanego odcinka:
Jeśli 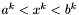 , to przechodzimy do kroku 3. W przeciwnym wypadku przechodzimy do kroku 9.
, to przechodzimy do kroku 3. W przeciwnym wypadku przechodzimy do kroku 9.
Krok 3:
Jeśli 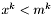 , przechodzimy do kroku 4. W przeciwnym wypadku przechodzimy do kroku 5.
, przechodzimy do kroku 4. W przeciwnym wypadku przechodzimy do kroku 5.
Krok 4:
Jeśli 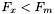 , redukujemy odcinek do
, redukujemy odcinek do ![$[a; \: m]$](form_398.png) :
:
![\[ a^{k+1} = a^k, \]](form_37.png)
![\[ m^{k+1} = x^k, \]](form_399.png)
![\[ b^{k+1} = m^k, \]](form_400.png)
![\[ F_b = F_m, \]](form_401.png)
![\[ F_m = F_x. \]](form_402.png)
Przechodzimy do kroku 6.
Jeśli 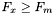 , redukujemy odcinek do
, redukujemy odcinek do ![$[x; \: b]$](form_404.png) :
:
![\[ a^{k+1} = x^k, \]](form_405.png)
![\[ m^{k+1} = m^k, \]](form_406.png)
![\[ b^{k+1} = b^k, \]](form_407.png)
![\[ F_a = F_x, \]](form_408.png)
Przechodzimy do kroku 6.
Krok 5:
Jeśli 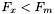 , redukujemy odcinek do
, redukujemy odcinek do ![$[m; \: b]$](form_409.png) :
:
![\[ a^{k+1} = m^k, \]](form_410.png)
![\[ m^{k+1} = x^k, \]](form_399.png)
![\[ b^{k+1} = b^k, \]](form_407.png)
![\[ F_a = F_m, \]](form_411.png)
![\[ F_m = F_x. \]](form_402.png)
Przechodzimy do kroku 6.
Jeśli 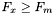 , redukujemy odcinek do
, redukujemy odcinek do ![$[a; \: x]$](form_412.png) :
:
![\[ a^{k+1} = a^k, \]](form_37.png)
![\[ m^{k+1} = m^k, \]](form_406.png)
![\[ b^{k+1} = x^k, \]](form_413.png)
![\[ F_b = F_x, \]](form_414.png)
Przechodzimy do kroku 6.
Krok 6:
Sprawdzamy długość odcinka po redukcji:
Jeśli 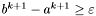 , przechodzimy do kroku 1. W przeciwnym wypadku przechodzimy do kroku 7.
, przechodzimy do kroku 1. W przeciwnym wypadku przechodzimy do kroku 7.
Krok 7:
Kończymy procedurę. Jeśli 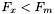 , wynikiem jest
, wynikiem jest 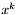 . W przeciwnym wypadku wynikiem jest
. W przeciwnym wypadku wynikiem jest 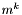 .
.
Krok 8:
Kończymy procedurę z komunikatem błędu: "Optymalizacja nie powiodła się - znaleziono maksimum lub punkt siodłowy funkcji aproksymującej."
Krok 9:
Kończymy procedurę z komunikatem błędu: "Optymalizacja nie powiodła się - znalezione minimum funkcji aproksymującej znajduje się poza badanym odcinkiem."
Metoda zaimplementowana na podstawie opisu zamieszczonego w:
Schwefel H.-P.: Evolution and Optimum Seeking. Nowy Jork, Wiley-Interscience 1995.