#include <SecantDivision.h>
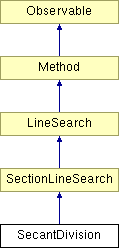
Diagram dziedziczenia dla SecantDivision

Metoda siecznych jest podobna do metod Bolzano i Newtona-Raphsona. Tak samo jak w metodzie Bolzano wykluczamy część przedziału i używamy do tego cely pochodnej, ale tym razem interesuje nas jej wartość. Każde kolejne przybliżenie punktu stacjonarnego wyliczamy ze wzoru:
![\[ x_{k+1} = x_k - f'(x_k) \frac{x_k-x_{k-1}}{f'(x_k)-f'(x_{k-1})} \]](form_479.png)
Jak można zauważyć drugi czynnik iloczynu jest odwrotnością numerycznego przybliżenia drugiej pochodnej funkcji celu, a więc wzór w zasadzie przybliża metodę Newtona-Rowsona.
Algorytm metody:
Oznaczenia:
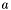 - lewy kraniec przedziału poszukiwań w danej iteracji
- lewy kraniec przedziału poszukiwań w danej iteracji
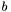 - prawy kraniec przedziału poszukiwań w danej iteracji
- prawy kraniec przedziału poszukiwań w danej iteracji
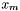 - bieżące przybliżenie punktu stacjonarnego
- bieżące przybliżenie punktu stacjonarnego
Dane potrzebne do obliczeń:
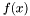 - minimalizowana funkcja jednej zmiennej
- minimalizowana funkcja jednej zmiennej
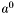 - lewy kraniec początkowego przedziału poszukiwań
- lewy kraniec początkowego przedziału poszukiwań
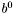 - prawy kraniec początkowego przedziału poszukiwań
- prawy kraniec początkowego przedziału poszukiwań
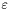 - wymagana dokładność rozwiązania
- wymagana dokładność rozwiązania
Krok 1:
Obliczyć 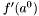 i
i 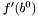 .
.
Krok 2:
Jeśli 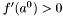 , a
, a 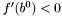 , zakończyć działanie algorytmu stwierdzając, że punkt stacjonarny nie znajduje się w przedziale początkowym.
, zakończyć działanie algorytmu stwierdzając, że punkt stacjonarny nie znajduje się w przedziale początkowym.
Krok 3:
Obliczyć:
![\[ x=b-f'(b) \frac{b-a}{f'(b)-f'(a)} \]](form_480.png)
Obliczyć pochodną w punkcie 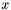
Krok 4a:
Jeśli 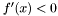 , to podstawić
, to podstawić 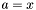 i przejść do kroku 5.
i przejść do kroku 5.
W przeciwnym wypadku przejść do kroku 4b.
Krok 4b:
Jeśli 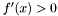 , to podstawić
, to podstawić 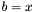 .
.
Przejść do kroku 5.
Krok 5:
Jeśli 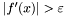 , przejść do kroku 3.
, przejść do kroku 3.
W przeciwnym wypadku zakończyć algorytm. Wynikiem jest ostatni punkt 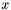 .
.
Algorytm zaimplementowano na podstawie:
Ostanin. A: Metody i algorytmy optymalizacji, Wydawnictwo Politechniki Białostockiej, Białystok, 2003