Dokumentacja klasy SignOfDerivative

#include <SignOfDerivative.h>

Diagram dziedziczenia dla SignOfDerivative

Opis szczegółowy

Metoda znaku pochodnej.

Metoda znaku pochodnej jest prostą metodą rozwiązywania problemów jednowymiarowych wykorzystującą znak pochodnej funkcji w punkcie.

Oznaczenia:
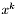$ x^k $ - punkt w danej iteracji
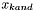$x_{kand}$ - kandydat na punkt w następnej iteracji
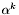$\alpha^k$ - współczynnik wpływu wartości pochodnej w punkcie na przesunięcie punktu roboczego

Dane potrzebne do obliczeń:
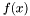$ f(x) $ - minimalizowana funkcja jednej zmiennej
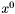$ x^0 $ - punkt poczatkowy
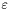$\varepsilon$ - wymagana dokładność rozwiązania
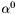$\alpha^0$ - początkowa wartość 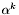$\alpha^k$ (może się zmniejszać gdy wykonywane kroki są za długie).
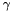$\gamma$ - współczynnik zmniejszania współczynnika 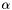$\alpha$ w przypadku, gdy wykonanie kroku dałoby gorszy wynik

Krok 1:
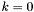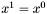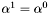Podstawić $ k=0 $ , $ x^1=x^0 $ oraz $\alpha^1 = \alpha^0$ .

Krok 2:
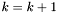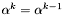Podstawić $ k=k+1 $ , a następnie $\alpha^k = \alpha^{k-1}$ .

Krok 3:
Obliczyć 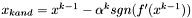$x_{kand} = x^{k-1} - \alpha^k sgn(f'(x^{k-1}))$ .
Jeśli 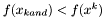$f(x_{kand}) < f(x^k)$ , podstawić 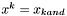$x^k=x_{kand}$ i przejść do kroku 5. W przeciwnym wypadku przejść do kroku 4.

Krok 4:
Zmniejszyć 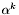$\alpha^k$ zgodnie ze wzorem: 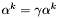$\alpha^k = \gamma \alpha^k$ , a następnie przejsć do kroku 3.

Krok 5:
Jeśli spełniony jest warunek zbieżności, zakoczyć działanie algorytmu i zwrócić 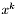$ x^k $ jako wynik. W przeciwnym wypadku przejść do kroku 2.

Algorytm zaimplementowano na podstawie pracy dyplomowej:
Grabowski J.: Numeryczne metody optymalizacji, miejsce i data obrony: Politechnika Wrocławska

Zobacz również:: LineSearch

Niniejszy dokument został półautomatycznie wycięty z dokumentacji kodu źródłowego programu Eduoptim 2. Pełna dokumentacja dostępna jest wraz ze źródłami bądź osobno w dziale pliki.
Hierarchia klas w programie nie odpowiada klasyfikacji metod optymalizacji.