#include <Simplex.h>
Diagram dziedziczenia dla Simplex

Metoda programowania liniowego służąca do rozwiązywania problemów w postaci standardowej:
![\[ \min \: \lbrace c^T x \; : \; Ax = b, \; x \ge 0 \rbrace, \]](form_489.png)
gdzie:
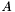 - macierz współczynników funkcji ograniczeń,
- macierz współczynników funkcji ograniczeń,
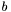 - wektor ograniczeń,
- wektor ograniczeń,
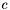 - wektor kosztów.
- wektor kosztów.
Metoda simplex oparta jest na spostrzeżeniu, że punkt, w którym znajduje się minimum, jest jednym z punktów wierzchołkowych obszaru dopuszczalnego i że da się go osiągnąć w skończonej liczbie kroków, przechodząc między punktami wierzchołkowymi w taki sposób, aby przy każdym przejściu wartość funkcji celu zmniejszała się.
Aby znajdować punkty wierzchołkowe, algorytm w kolejnych iteracjach wyróżnia w macierzy 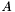 część bazową i niebazową oraz rozwiązuje układy równań
część bazową i niebazową oraz rozwiązuje układy równań 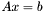 względem bazowych współczynników punktu
względem bazowych współczynników punktu 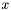 (niebazowe współczynniki traktuje się jako zerowe).
(niebazowe współczynniki traktuje się jako zerowe).
W ten sposób w każdym etapie wyznaczany jest jeden punkt znajdujący się na przecięciu ograniczeń związanych z aktualną bazą. Na końcu każdego etapu w bazie wymienia się jedną zmienną: wprowadza się tą ze zmiennych niebazowych, której wzrost prowadzi do najszybszego spadku funkcji celu, a wyprowadza tą ze zmiennych bazowych, która po wprowadzeniu nowej zmiennej najszybciej osiąga wartość 0 (pamiętajmy, że standardowe sformułowanie problemu narzuca ograniczenie 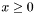 ).
).
Algorytm kończy się, gdy wprowadzenie żadnej ze zmiennych niebazowych do bazy nie będzie mogło prowadzić do spadku wartości funkcji celu.
Zaimplementowano dwufazową wersję algorytmu - jeśli wyznaczenie pierwszej bazy nie jest trywialne (macierz 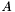 nie jest w postaci kanonicznej), metoda w celu znalezienia bazy tworzy problem rozszerzony (macierze
nie jest w postaci kanonicznej), metoda w celu znalezienia bazy tworzy problem rozszerzony (macierze 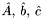 ) i rozwiązuje go przy pomocy algorytmu simplex.
) i rozwiązuje go przy pomocy algorytmu simplex.
Informacje wejściowe:
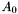 - macierz współczynników funkcji ograniczeń [
- macierz współczynników funkcji ograniczeń [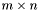 ],
],
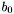 - wektor ograniczeń [
- wektor ograniczeń [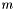 ],
],
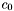 - wektor kosztów (współczynników funkcji celu) [
- wektor kosztów (współczynników funkcji celu) [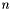 ].
].
Oznaczenia:
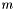 - liczba ograniczeń (liczba wierszy macierzy
- liczba ograniczeń (liczba wierszy macierzy 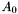 ),
),
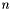 - liczba zmiennych (uwzględnia zmienne dopełniające, nie uwzględnia zmiennych rozszerzających, liczba kolumn macierzy
- liczba zmiennych (uwzględnia zmienne dopełniające, nie uwzględnia zmiennych rozszerzających, liczba kolumn macierzy 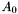 ),
),
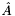 - macierz wsp. f. ograniczeń problemu rozszerzonego [
- macierz wsp. f. ograniczeń problemu rozszerzonego [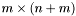 ],
],
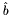 - wektor ograniczeń problemu rozszerzonego [
- wektor ograniczeń problemu rozszerzonego [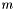 ],
],
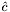 - wektor kosztów problemu rozszerzonego [
- wektor kosztów problemu rozszerzonego [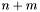 ],
],
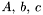 - macierze aktualnie rozwiązywanego problemu,
- macierze aktualnie rozwiązywanego problemu,
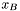 - wektor bazowych współrzędnych aktualnego punktu [
- wektor bazowych współrzędnych aktualnego punktu [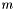 ],
],
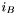 - wektor indeksów bazowych (indeksów kolumn macierzy
- wektor indeksów bazowych (indeksów kolumn macierzy 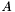 , które tworzą aktualną bazę),
, które tworzą aktualną bazę),
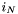 - wektor indeksów niebazowych,
- wektor indeksów niebazowych,
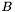 - aktualna baza (macierz zbudowana z kolumn macierzy
- aktualna baza (macierz zbudowana z kolumn macierzy 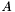 o indeksach z
o indeksach z 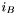 ) [
) [ ],
],
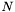 - macierz zbudowana z pozostałych, niebazowych kolumn
- macierz zbudowana z pozostałych, niebazowych kolumn 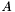 [
[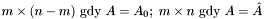 ],
],
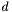 - wektor kosztów zredukowanych (zawiera informację o wpływie ewentualnego wprowadzenia danej zmiennej niebazowej na wartość funkcji celu) [
- wektor kosztów zredukowanych (zawiera informację o wpływie ewentualnego wprowadzenia danej zmiennej niebazowej na wartość funkcji celu) [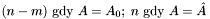 ],
],
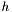 - wektor przesunięcia (zawiera informację o tym, jak proporcjonalnie zmienią się poszczególne zmienne bazowe po wprowadzeniu nowej zmiennej do bazy) [
- wektor przesunięcia (zawiera informację o tym, jak proporcjonalnie zmienią się poszczególne zmienne bazowe po wprowadzeniu nowej zmiennej do bazy) [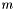 ],
],
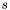 - indeks zmiennej wprowadzanej do bazy,
- indeks zmiennej wprowadzanej do bazy,
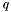 - indeks zmiennej wyprowadzanej z bazy,
- indeks zmiennej wyprowadzanej z bazy,
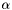 - długość kroku przy przejściu do nowego punktu wierzchołkowego,
- długość kroku przy przejściu do nowego punktu wierzchołkowego,
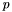 - informacja o aktualnie przeprowadzanej fazie algorytmu (
- informacja o aktualnie przeprowadzanej fazie algorytmu (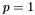 - faza wstępna: rozwiązywanie problemu rozszerzonego w celu znalezienia pierwszej bazy;
- faza wstępna: rozwiązywanie problemu rozszerzonego w celu znalezienia pierwszej bazy; 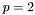 - rozwiązywanie problemu właściwego) .
- rozwiązywanie problemu właściwego) .
Procedura.
Krok 1:
Sprawdzamy, czy ostatnich 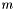 kolumn macierzy
kolumn macierzy 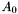 tworzy macierz identycznościową. Jeśli tak, przechodzimy do kroku 2. Jeśli nie, przechodzimy do kroku 3.
tworzy macierz identycznościową. Jeśli tak, przechodzimy do kroku 2. Jeśli nie, przechodzimy do kroku 3.
Krok 2:
Macierz bazowa będzie utworzona z ostatnich 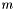 kolumn macierzy
kolumn macierzy 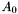 .
.
Podstawiamy:
![\[ i_B = \lbrack n - m + 1, \: n - m + 2, \: \ldots, \: n \rbrack , \]](form_516.png)
![\[ i_N = \lbrack 1, \: 2, \: \ldots, \: n - m \rbrack . \]](form_517.png)
Przechodzimy do kroku 5.
Krok 3:
W celu znalezienia pierwszej bazy rozwiązujemy problem rozszerzony.
Tworzymy macierze problemu rozszerzonego:
![\[ A = \lbrack A_0 \; | \; I(m) \rbrack = \hat{A} , \]](form_518.png)
![\[ b = b_0 = \hat{b} , \]](form_519.png)
![\[ c = \lbrack 0(n) \; | \; 1(m) \rbrack = \hat{c} , \]](form_520.png)
gdzie:
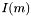 - macierz jednostkowa
- macierz jednostkowa 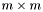 ,
,
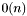 - wektor zerowy o
- wektor zerowy o 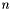 wersach,
wersach,
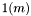 - wektor jednostkowy o
- wektor jednostkowy o 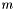 wersach.
wersach.
Podstawiamy:
![\[ i_B = \lbrack n + 1, \: n + 2, \: \ldots, \: n + m \rbrack , \]](form_524.png)
![\[ i_N = \lbrack 1, \: 2, \: \ldots, \: n \rbrack . \]](form_525.png)
Na podstawie 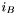 i
i 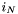 oraz
oraz 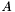 tworzymy macierze
tworzymy macierze 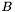 i
i 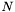 .
.
Podstawiamy 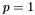 i przechodzimy do kroku 6.
i przechodzimy do kroku 6.
Krok 4:
Sprawdzamy, czy otrzymane po rozwiązaniu problemu rozszerzonego indeksy bazowe są poprawne (nie dotyczą kolumn rozszerzających):
Jeśli 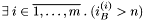 , to STOP - zmiennych rozszerzających nie udało się wyeliminować, problemu nie da się rozwiązać.
, to STOP - zmiennych rozszerzających nie udało się wyeliminować, problemu nie da się rozwiązać.
W przeciwnym wypadku usuwamy niebazowe indeksy zmiennych rozszerzających :
dla 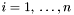 jeśli
jeśli 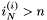 , element ten jest usuwany z wektora.
, element ten jest usuwany z wektora.
Przechodzimy do kroku 5.
Krok 5:
Podstawiamy:
![\[ A = A_0, \]](form_529.png)
![\[ b = b_0, \]](form_530.png)
![\[ c = c_0, \]](form_531.png)
![\[ p = 2 . \]](form_532.png)
Na podstawie 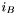 i
i 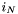 oraz
oraz  tworzymy macierze
tworzymy macierze  i
i 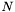 .
.
Przechodzimy do kroku 6.
Krok 6:
Obliczamy macierz odwrotną do bazowej 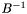 .
.
Wyznaczamy pierwszy punkt wierzchołkowy:
![\[ x_B = B^{-1} b .\]](form_534.png)
Przechodzimy do kroku 7.
Krok 7:
Obliczamy wektor kosztów zredukowanych:
![\[ d = c_N - N^T B^{-T} c_B . \]](form_535.png)
Sprawdzamy warunek stopu:
Jeśli 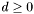 , to: jeśli
, to: jeśli 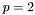 to STOP - wynikiem jest
to STOP - wynikiem jest 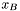 uzupełniony o pozostałe, niebazowe zmienne; jeśli
uzupełniony o pozostałe, niebazowe zmienne; jeśli 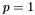 , to przechodzimy do kroku 4.
, to przechodzimy do kroku 4.
Jeśli 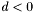 , to zapamiętujemy indeks najmniejszej składowej tego wektora - będzie to indeks zmiennej wprowadzanej do bazy:
, to zapamiętujemy indeks najmniejszej składowej tego wektora - będzie to indeks zmiennej wprowadzanej do bazy:
![\[ s = \arg \min_{i \in \overline{1,\ldots,dim(d)}} d^{(i)} . \]](form_538.png)
Przechodzimy do kroku 8.
Krok 8:
Obliczamy wektor przesunięcia:
![\[ h = B^{-1} N^{(s)} , \]](form_539.png)
gdzie:
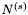 - s-ta kolumna macierzy
- s-ta kolumna macierzy 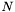 .
.
Sprawdzamy, czy 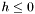 . Jeśli tak, to STOP - problem jest nieograniczony.
. Jeśli tak, to STOP - problem jest nieograniczony.
W przeciwnym wypadku szukamy zmiennej, którą należy wyprowadzić z bazy:
![\[ \mbox{Dla } i = 1, \: \ldots, \: m \mbox{: } \; \sigma^{(i)} = \left\{ \begin{array}{ll} \frac{x_B^{(i)}}{h^{(i)}} & \mbox{ dla $h^{(i)} > 0$} \\ +\infty & \mbox{ dla $h^{(i)} \le 0$} \end{array} \right. \]](form_542.png)
![\[ q = \arg \min_{i \in \overline{1,\ldots,m}} \sigma^{(i)} , \]](form_543.png)
![\[ \alpha = \sigma^{(q)} . \]](form_544.png)
Przechodzimy do kroku 9.
Krok 9:
Zamieniamy indeksy zmiennej wychodzącej i wchodzącej do bazy:
![\[ i_B^{(q)} \leftrightarrow i_N^{(s)}. \]](form_545.png)
Na podstawie nowych indeksów tworzymy macierze 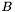 i
i 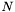 .
.
Obliczamy nową macierz 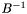 .
.
Wyznaczamy nowy punkt wierzchołkowy:
![\[ x_B = x_B - \alpha h, \]](form_546.png)
![\[ x_B^{(q)} = \alpha. \]](form_547.png)
Przechodzimy do kroku 7.
Uwagi.
Zaimplementowano metodę niezmodyfikowaną, bez algorytmu zapobiegającego zapętleniu przy występowaniu punktów zdegenerowanych.
Metoda zaimplementowana na podstawie opisu zamieszczonego w:
Bruun H. N.: Algorithms for Linear Optimization - an Introduction. Lyngby, Technical University of Denmark 1999.
(http://www2.imm.dtu.dk/courses/02611/ALO.pdf).