Dokumentacja klasy BolzanoDivision

#include <BolzanoDivision.h>

Diagram dziedziczenia dla BolzanoDivision

Opis szczegółowy

Metoda podziału Bolzano.

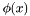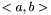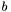Metoda BolzanoDivision (inaczej: metoda punktu środkowego) działa przy wykorzystaniu twierdzenia BolzanoDivision-Cauchy'ego, które brzmi: Niech funkcja $\phi(x)$ będzie określona i ciągła w przedziale domkniętym $ <a,b> $ i niech na końcach tego przedziału przyjmuje wartości różnych znaków. Wówczas pomiędzy $ a $ i $ b $ znajduje się punkt c, w którym funkcja równa się zeru:

$\phi(c)=0, a<c<b$

W naszym przypadku funkcją 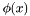$\phi(x)$ jest pochodna funkcji celu $ f'(x) $ .

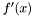Algorytm metody:

Oznaczenia:
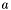$ a $ - lewy kraniec przedziału poszukiwań w danej iteracji
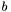$ b $ - prawy kraniec przedziału poszukiwań w danej iteracji
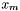$ x_m $ - punkt w połowie przedziału nieoznaczoności w danej iteracji

Dane potrzebne do obliczeń:
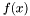$ f(x) $ - minimalizowana funkcja jednej zmiennej
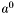$ a^0 $ - lewy kraniec początkowego przedziału poszukiwań
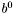$ b^0 $ - prawy kraniec początkowego przedziału poszukiwań
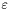$\varepsilon$ - wymagana dokładność rozwiązania

Krok 1:
Obliczyć 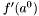$ f'(a^0) $ i $ f'(b^0) $ .

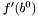Krok 2:
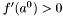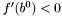Jeśli $ f'(a^0)>0 $ , a $ f'(b^0)<0 $ , zakończ działanie algorytmu stwierdzając, że punkt stacjonarny nie znajduje się w przedziale początkowym.
W przeciwnym wypadku przejść do kroku 3.

Krok 3:
Oblicz: 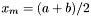$ x_m=(a+b)/2 $ oraz pochodną w tym punkcie $ f'(x_m) $ .

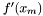Krok 4:
Jeśli 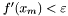$f'(x_m)<\varepsilon$ , zakończ działanie algorytmu. Wynikiem jest punkt $ x_m $ .

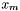Krok 5a:
Jeśli 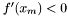$ f'(x_m)<0 $ , podstaw 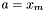$ a=x_m $ i przejdź do kroku 3.
W przeciwnym wypadku przejdź do kroku 5b.

Krok 5b:
Podstaw 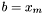$ b=x_m $ i przejdź do kroku 3.

Algorytm zaimplementowano na podstawie:
Ostanin. A: Metody i algorytmy optymalizacji, Wydawnictwo Politechniki Białostockiej, Białystok, 2003

Zobacz również:: Linesearch

Niniejszy dokument został półautomatycznie wycięty z dokumentacji kodu źródłowego programu Eduoptim 2. Pełna dokumentacja dostępna jest wraz ze źródłami bądź osobno w dziale pliki.
Hierarchia klas w programie nie odpowiada klasyfikacji metod optymalizacji.