Dokumentacja klasy DFP

#include <DFP.h>

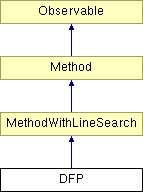
Diagram dziedziczenia dla DFP

Opis szczegółowy

Metoda Davidona-Fletchera-Powella.

Metoda zmiennej metryki.
Metoda z rodziny algorytmów quasi-Newtonowskich, opartych na tej samej własności i sposobie postępowania, co zmodyfikowana metoda Newtona: dla funkcji celu o postaci

$f(x) = q + b^T x + \frac{1}{2} x^T A x$

wystarczy znajomość macierzy odwrotnej do hesjanu 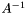$A^{-1}$ , aby w jednym kroku wyznaczyć minimum. Poszukiwanie przebiega wtedy zgodnie z prostą procedurą:

$x^{k+1} = x^k - \tau A^{-1} \nabla f(x^k).$

Metody quasi-Newtonowskie zastępują macierz 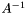$A^{-1}$ , której otrzymanie jest kosztowne ze względu na konieczność wyliczania drugich pochodnych, macierzą estymującą 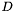$D$ . Staje się ona w kolejnych iteracjach coraz lepszym przybliżeniem macierzy odwrotnej do hesjanu. Pierwszym, ale efektywnym pomysłem na generowanie takiej macierzy był wzór Davidona-Fletchera-Powella:

$D^{k+1} = D^k + \frac{p^k (p^k)^T}{(p^k)^T q^k} - \frac{D^k q^k (q^k)^T D^k}{(q^k)^T D^k q^k},$

gdzie:

$p^k = x^{k+1} - x^k,$

$q^k = \nabla f(x^{k+1}) - \nabla f(x^k).$

Gdy przybliżenie uznaje się za zadowalające, procedura kończy się.

Informacje wejściowe:
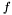$f$ - minimalizowana funkcja 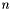$n$ zmiennych,
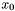$x_0$ - dowolnie wybrany punkt startowy,
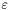$\varepsilon$ - wymagana dokładność obliczeń,
warunek stopu - do wyboru:

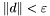
$\|d\| < \varepsilon$
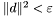
$\|d\|^2 < \varepsilon$
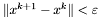$\|x^{k+1} - x^k\| < \varepsilon$ ,
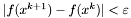$|f(x^{k+1}) - f(x^k)| < \varepsilon$ ,
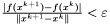$\frac{|f(x^{k+1}) - f(x^k)|}{\|x^{k+1} - x^k\|} < \varepsilon$ ,

wybrana metoda minimalizacji w kierunku wraz z parametrami,
informacja, czy realizowana będzie metoda z modyfikacją.

Oznaczenia:
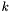$k$ - numer aktualnej iteracji,
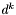$d^k$ - aktualny kierunek poszukiwań,
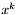$x^k$ - aktualny punkt,
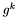$g^k$ - gradient funkcji w punkcie $x^k$ ,
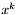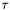$\tau$ - długość wykonywanego aktualnie kroku,
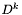$D^k$ - aktualna macierz estymująca m. odwrotną do hesjanu.

Procedura.

Krok wstępny:
Podstawiamy:

$D^1 = I(n), \mbox{ gdzie } I(n) - \mbox{ macierz jednostkowa } n \times n ,$

$g^0 = \nabla f(x^0),$

$g^1 = g^0,$

$d^1 = -g^0,$

$x^1 = x^0,$

$k = 1.$

Krok 1:
Sprawdzamy warunek stopu.
Jeśli jest on spełniony, to STOP. Wynikiem jest 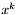$x^k$ .
W przeciwnym wypadku przechodzimy do kroku 2.

Krok 2:
Wykonujemy krok o optymalnej długości 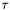$\tau$ w aktualnym kierunku:

$\tau = \arg \min_{\tau} f(x^k + \tau d^k) ,$

$x^{k+1} = x^k + \tau d^k .$

Obliczamy gradient w otrzymanym punkcie:

$g^{k+1} = \nabla f(x^{k+1}) .$

Przechodzimy do kroku 3.

Krok 3:
Jeśli realizowana jest wersja z modyfikacją, sprawdzamy, czy 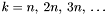$k = n, \: 2n, \: 3n, \: \ldots$ . Jeśli tak, podstawiamy:

$D^{k+1} = I(n)$

i przechodzimy do kroku 5.

W przeciwnym razie przechodzimy do kroku 4.

Krok 4:
Wyliczamy 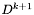$D^{k+1}$ jako kolejne przybliżenie macierzy odwrotnej do hesjanu, zgodnie ze wzorem Davidona-Fletchera-Powella:

$D^{k+1} = D^k + \frac{p^k (p^k)^T}{(p^k)^T q^k} - \frac{D^k q^k (q^k)^T D^k}{(q^k)^T D^k q^k},$

gdzie:

$p^k = x^{k+1} - x^k,$

$q^k = g^{k+1} - g^k.$

Krok 5:
Wyznaczamy kolejny kierunek:

$d^{k+1} = -D^{k+1} g^{k+1} .$

Podstawiamy 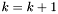$ k = k + 1 $ i przechodzimy do kroku 1.

Uwagi.
Metody zmiennej metryki należą do najwydajniejszych algorytmów optymalizacji bez ograniczeń. Ze względu jednak na konieczność stopniowego estymowania macierzy odwrotnej do hesjanu, w niektórych wypadkach mogą być one wolniej zbieżne od zmodyfikowanej metody Newtona (w zamian za większą liczbę kroków potrzebnych do znalezienia minimum otrzymamy jednak znacznie mniejszą liczbę wyliczeń funkcji celu).

Regularne ponowne inicjowanie macierzy 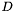$D$ macierzą jednostkową (krok 3) wprowadzono w celu zwiększenia stabilności metody. Gdyby aktualizować macierz zgodnie ze wzorem Davidona-Fletchera-Powella w każdej iteracji, mogłaby ona stracić, na skutek niedokładnych obliczeń i niedokładności metody minimalizacji w kierunku, dodatnią określoność, a to mogłoby doprowadzić do dążenia algorytmu w kierunku maksimum. Ceną za poprawę stabilności w taki sposób jest oczywiście mniejsza szybkość zbieżności metody.

Metoda zaimplementowana na podstawie opisu zamieszczonego w:
Findeisen W., Szymanowski J., Wierzbicki A.: Teoria i metody obliczeniowe optymalizacji. Warszawa, PWN 1977.

Zobacz również:: MethodWithLineSearch
NewtonModified

Niniejszy dokument został półautomatycznie wycięty z dokumentacji kodu źródłowego programu Eduoptim 2. Pełna dokumentacja dostępna jest wraz ze źródłami bądź osobno w dziale pliki.
Hierarchia klas w programie nie odpowiada klasyfikacji metod optymalizacji.