Dokumentacja klasy NewtonModified

#include <NewtonModified.h>

Diagram dziedziczenia dla NewtonModified

Opis szczegółowy

Zmodyfikowana metoda Newtona.

Przy wykorzystaniu do minimalizacji funkcji niekwadratowych metoda Newtona nie jest niezawodna. Gdy punkt startowy znajduje się daleko od minimum, krok metody może okazać się zbyt duży, co z kolei może doprowadzić do niezbieżności metody. Najprostszą modyfikacją metody Newtona jest wprowadzenie etapu poszukiwania optymalnej długości kroku w kierunku 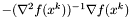$-(\nabla^2 f(x^k))^{-1} \nabla f(x^k)$ , podobnie jak w metodzie Cauchy'ego (największego spadku). Zapewnia to zmniejszanie się wartości funkcji w punkcie roboczym z kroku na krok.

Algorytm metody:

Oznaczenia:
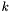$ k $ - numer aktualnej iteracji
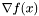$\nabla f(x)$ - gradient w punkcie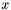 $ x $
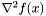$\nabla^2 f(x)$ - macierz hesjanu w punkcie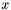 $ x $
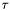$\tau$ - współczynnik długości kroku

Dane potrzebne do obliczeń:
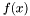$ f(x) $ - minimalizowana funkcja celu
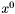$ x^0 $ - punkt startowy
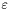$\varepsilon$ - wymagana dokładność
warunek stopu - do wyboru:

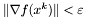
$\|\nabla f(x^k)\| < \varepsilon$
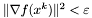
$\|\nabla f(x^k)\|^2 < \varepsilon$
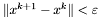$\|x^{k+1} - x^k\| < \varepsilon$ ,
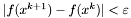$|f(x^{k+1}) - f(x^k)| < \varepsilon$ ,
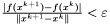$\frac{|f(x^{k+1}) - f(x^k)|}{\|x^{k+1} - x^k\|} < \varepsilon$ ,

wybrana metoda minimalizacji w kierunku wraz z parametrami.

Krok 0 (wstępny):
Podstaw $ k=0 $

.

Krok 1:
Sprawdź czy spełniony jest warunek stopu. Jeśli tak, to przerwij działanie algorytmu i przedstaw $ x^k $

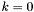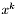jako wynik. W przeciwnym wypadku przejdź do kroku 2.

Krok 2:
Sprawdź czy:

$| \nabla^2 f(x^k)) | = 0$

Jeśli tak to STOP: Hesjan jest macierzą osobliwą.
W przeciwnym wypadku przejdź do kroku 3.

Krok 3:
Wyznacz kierunek poszukiwań 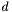$d$ :

$d = -(\nabla^2 f(x^k))^{-1} \nabla f(x^k).$

Wykonaj krok w kierunku 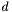$d$ o optymalnej długości $\tau$ :

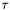$\tau = \arg \min_{\tau} f(x^k + \tau d),$

$x^{k+1} = x^k + \tau d.$

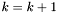Podstaw $ k=k+1 $ i przejdź do kroku 1.

Uwagi:
W stosunku do wersji algorytmu zamieszczonej w [1] zmieniono kolejność wykonywania kroków. W zaimplementowanej wersji sprawdzanie warunku stopu dokonuje się na początku każdej iteracji. Dzięki temu algorytm może zatrzymać się nie wykonując żadnej iteracji w przypadku gdy punkt startowy znajduje sie w minimum i wykorzystywany jest "gradientowy" warunek stopu. Początkowe wartości zmiennych oznaczających rożnice położenia dwóch ostatnich punktów oraz różnice wartości funkcji w tych dwóch punktach są równe DBL_MAX, więc w przypadku wykorzystaniu innego warunku stopu niż "gradientowy" modyfikacja nie będzie miała żadnego wpływu na działanie algorytmu.

Algorytm zaimplementowano na podstawie:
Ostanin. A: Metody i algorytmy optymalizacji, Wydawnictwo Politechniki Białostockiej, Białystok, 2003

Zobacz również:: Newton

Niniejszy dokument został półautomatycznie wycięty z dokumentacji kodu źródłowego programu Eduoptim 2. Pełna dokumentacja dostępna jest wraz ze źródłami bądź osobno w dziale pliki.
Hierarchia klas w programie nie odpowiada klasyfikacji metod optymalizacji.