Dokumentacja klasy Newton

#include <Newton.h>

Diagram dziedziczenia dla Newton

Opis szczegółowy

Metoda Newtona.

Podstawą metody Newtona jest aproksymacja funkcji celu funkcją kwadratową. Algorytm wyznacza każdy następny punkt w taki sposób by gradient kwadratowej funkcji aproksymującej wynosił w nim 0.

Przy zastosowaniu metody Newtona i przy niewystępowaniu niedokładności numerycznych, funkcje kwadratowe minimalizowane są w jednej iteracji. W przypadku gdy funkcja celu nie jest kwadratowa i gdy punkt startowy znajduje się w znacznej odległości od minimum, metoda Newtona charakteryzuje się wolną zbieżnością, lub nawet jej brakiem.

Algorytm metody:

Oznaczenia:
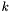$ k $ - numer aktualnej iteracji
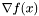$\nabla f(x)$ - gradient w punkcie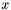 $ x $
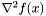$\nabla^2 f(x)$ - macierz hesjanu w punkcie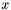 $ x $

Dane potrzebne do obliczeń:
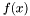$ f(x) $ - minimalizowana funkcja celu
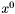$ x^0 $ - punkt startowy
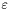$\varepsilon$ - wymagana dokładność,
warunek stopu - do wyboru:

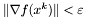
$\|\nabla f(x^k)\| < \varepsilon$
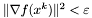
$\|\nabla f(x^k)\|^2 < \varepsilon$
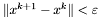$\|x^{k+1} - x^k\| < \varepsilon$ ,
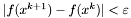$|f(x^{k+1}) - f(x^k)| < \varepsilon$ ,
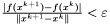$\frac{|f(x^{k+1}) - f(x^k)|}{\|x^{k+1} - x^k\|} < \varepsilon$ .

Krok 0 (wstępny):
Podstaw $ k=0 $

.

Krok 1:
Sprawdź czy spełniony jest warunek stopu. Jeśli tak, to przerwij działanie algorytmu i przedstaw $ x^k $

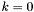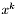jako wynik. W przeciwnym wypadku przejdź do kroku 2.

Krok 2:
Sprawdź czy:

$| \nabla^2 f(x^k)) | = 0$

Jeśli tak to STOP: Hejsan jest macierzą osobliwą.
W przeciwnym wypadku przejdź do kroku 3.

Krok 3:
Oblicz:

$x^{k+1} = x^k - (\nabla^2 f(x^k))^{-1} \nabla f(x^k)$

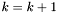Podstaw $ k=k+1 $ i przejdź do kroku 1.

Uwagi:
W stosunku do wersji algorytmu zamieszczonej w [1] zmieniono kolejność wykonywania kroków. W zaimplementowanej wersji sprawdzanie warunku stopu dokonuje się na początku każdej iteracji. Dzięki temu algorytm może zatrzymać się nie wykonując żadnej iteracji w przypadku gdy punkt startowy znajduje sie w minimum i wykorzystywany jest "gradientowy" warunek stopu. Początkowe wartości zmiennych oznaczających rożnice położenia dwóch ostatnich punktów oraz różnice wartości funkcji w tych dwóch punktach są równe DBL_MAX, więc w przypadku wykorzystaniu innego warunku stopu niż "gradientowy" modyfikacja nie będzie miała żadnego wpływu na działanie algorytmu.

[1] Aleksander Ostanin - Metody i algorytmy optymalizacji, Wydawnictwo Politechniki Białostockiej, Białystok 2003

Zobacz również:: NewtonModified

Niniejszy dokument został półautomatycznie wycięty z dokumentacji kodu źródłowego programu Eduoptim 2. Pełna dokumentacja dostępna jest wraz ze źródłami bądź osobno w dziale pliki.
Hierarchia klas w programie nie odpowiada klasyfikacji metod optymalizacji.