Dokumentacja klasy HookeJeevesDiscrete

#include <HookeJeevesDiscrete.h>

Diagram dziedziczenia dla HookeJeevesDiscrete

Opis szczegółowy

Metoda Hooke'a i Jeevesa z krokiem dyskretnym.

Metoda poszukiwań prostych.
Metoda wyznacza kierunek za pomocą kroków próbnych wzdłuż osi, a następnie wykonuje krok roboczy w tym kierunku. Jeśli w nowym punkcie, za pomocą kolejnych kroków próbnych, uda się wyznaczyć kierunek opadania funkcji, wykonywany jest kolejny krok roboczy. Jeśli nie, to długość kroku próbnego (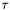 $\tau$ ) jest zmniejszana (mnożona razy współczynnik $\beta$ ).

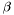Algorytm kończy się w momencie, gdy długość kroku staje się mniejsza niż parametr epsilon lub przekroczona zostaje dozwolona liczba iteracji.

Informacje wejściowe:
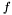$f$ - minimalizowana funkcja 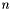$n$ zmiennych,
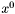$x^0$ - dowolnie wybrany punkt startowy,
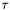$\tau$ : - długość kroku próbnego,
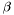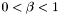$\beta$ - współczynnik skracania kroku ( $0 < \beta < 1$ ),
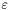$\varepsilon$ - warunek stopu - minimalna długość kroku próbnego.

Oznaczenia:
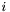$i$ - indeks aktualnego kierunku,
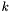$k$ - numer aktualnej iteracji,
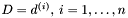$D = d^{(i)},\: i=1,\ldots,n$ - aktualna baza kierunków,
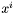$x^i$ - aktualny punkt próbny,
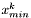$x^k_{min}$ - najlepszy punkt w k-tym etapie,
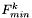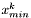$F^k_{min}$ - wartość funkcji w punkcie $x^k_{min}$ ,
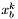$x_b^k$ - punkt bazowy dla kroków próbnych w k-tym etapie,
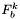$F^k_b$ - wartość funkcji w punkcie $x^k_b$ .

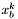Procedura.

Krok wstępny:
Podstawiamy:

$D = I(n), \mbox{ gdzie } I(n) - \mbox{ macierz jednostkowa } n \times n ,$

$x^1_{min} = x^0,$

$F^1_{min} = f(x^0) ,$

$x_b^1 = x^0,$

$F_b^1 = f(x^0) ,$

$k = 1 ,$

$i = 1 .$

Krok 1:
Badamy wartość funkcji w nowym punkcie próbnym po wykonaniu kroku w i-tym kierunku (wzdłuż i-tej osi):

$x^i = x^k_{min} + \tau d^{(i)} .$

Jeśli krok był udany (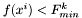 $f(x^i) < F^k_{min}$ ), to zapamiętujemy punkt próbny jako najlepszy:

$x^k_{min} = x^i,$

$F^k_{min} = f(x^i),$

a następnie przechodzimy do kroku 3.
W przeciwnym wypadku (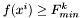 $f(x^i) \ge F^k_{min}$ ) przechodzimy do kroku 2.

Krok 2:
Wykonujemy krok próbny w przeciwnym kierunku:

$x^i = x^k_{min} - \tau d^{(i)} .$

Jeśli krok był udany (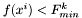 $f(x^i) < F^k_{min}$ ), to zapamiętujemy punkt próbny jako najlepszy:

$x^k_{min} = x^i,$

$F^k_{min} = f(x^i).$

Przechodzimy do kroku 3.

Krok 3:
Sprawdzamy, czy wykonano kroki próbne we wszystkich kierunkach:
Jeśli 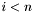$i < n$ , podstawiamy 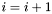$i = i + 1$ i ponownie przechodzimy do kroku 1.
Jeśli 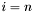$i = n$ , przechodzimy do kroku 4.

Krok 4:
Sprawdzamy, czy przy ostatnim przeszukiwaniu 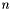$n$ kierunków nastąpiła poprawa:
Jeśli tak (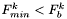 $F^k_{min} < F_b^k$ ), to przechodzimy do kroku 5.
W przeciwnym razie przechodzimy do kroku 6.

Krok 5:
Zapamiętujemy aktualny punkt jako punkt bazowy dla następnego etapu:

$x_b^{k+1} = x^k_{min}.$

Następnie wykonujemy krok roboczy w znalezionym w tym etapie kierunku opadania funkcji:

$x^{k+1}_{min} = x^k_{min} + (x^k_{min} - x^k_b).$

Przechodzimy do kroku 7.

Krok 6:
Skracamy długość kroku próbnego:

$\tau = \beta \tau$

i cofamy się do punktu bazowego:

$x^{k+1}_{min} = x^k_b.$

Przechodzimy do kroku 7.

Krok 7:
Sprawdzamy warunek stopu:
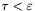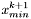Jeśli $\tau < \varepsilon$ , kończymy działanie. Wynikiem jest $x^{k+1}_{min}$ .
W przeciwnym wypadku podstawiamy 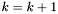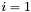$k = k+1$ , $i = 1$ i przechodzimy do kroku 1.

Uwagi.
Metoda zaimplementowana na podstawie programu Marka G. Johnsona (http://www.netlib.org/opt/hooke.c), który powstał na podstawie pseudokodu z "Algorithm 178: Direct Search" Arthura F. Kaupe Jr. i zawiera poprawki Bella i Pike'a (CACM v.9, str. 684, Wrzesień 1966) oraz Tomlina i Smitha ("Remark on Algorithm 178", CACM v.12).

Długość kroków próbnych nie jest zależna od pozycji punktu startowego, w przeciwieństwie do implementacji Johnsona.

Zobacz również:: HookeJeevesOptimal

Niniejszy dokument został półautomatycznie wycięty z dokumentacji kodu źródłowego programu Eduoptim 2. Pełna dokumentacja dostępna jest wraz ze źródłami bądź osobno w dziale pliki.
Hierarchia klas w programie nie odpowiada klasyfikacji metod optymalizacji.