Dokumentacja klasy HookeJeevesOptimal

#include <HookeJeevesOptimal.h>

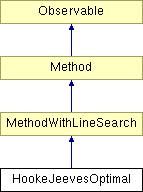
Diagram dziedziczenia dla HookeJeevesOptimal

Opis szczegółowy

Metoda Hooke'a i Jeevesa z krokiem optymalnym.

Metoda wyznacza kierunek za pomocą kroków próbnych wzdłuż osi, a następnie wykonuje krok roboczy w tym kierunku. W odróżnieniu od pierwotnej wersji metody, w tym wariancie długości kroków próbnych i roboczego są wyznaczane przez metodę optymalizacji w kierunku. Oznacza to, że każdy krok jest udany, dlatego nigdy nie ma potrzeby cofania się do punktu bazowego.

Warunek stopu jest oparty na porównaniu dwóch ostatnich kroków, zastosowana może być jedna z klas pochodnych StandardStopCondition.

Informacje wejściowe:
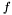$f$ - minimalizowana funkcja 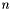$n$ zmiennych,
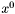$x^0$ - dowolnie wybrany punkt startowy,
warunek stopu - do wyboru:

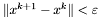$\|x^{k+1} - x^k\| < \varepsilon$ ,
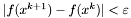$|f(x^{k+1}) - f(x^k)| < \varepsilon$ ,
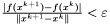$\frac{|f(x^{k+1}) - f(x^k)|}{\|x^{k+1} - x^k\|} < \varepsilon$ ,

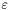$\varepsilon$ - dokładność,
wybrana metoda minimalizacji w kierunku wraz z parametrami.

Oznaczenia:
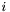$i$ - indeks aktualnego kierunku,
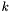$k$ - numer aktualnej iteracji,
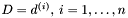$D = d^{(i)},\: i=1,\ldots,n$ - aktualna baza kierunków,
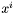$x^i$ - aktualny punkt próbny,
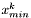$x^k_{min}$ - najlepszy punkt w k-tym etapie,
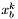$x_b^k$ - punkt bazowy dla kroków próbnych w k-tym etapie,
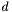$d$ - kierunek kroku roboczego.

Procedura.

Krok wstępny:
Podstawiamy:

$D = I(n), \mbox{ gdzie } I(n) - \mbox{ macierz jednostkowa } n \times n ,$

$x^1_{min} = x^0,$

$x_b^1 = x^0,$

$k = 1 ,$

$i = 1 .$

Krok 1:
Przy pomocy metody optymalizacji w kierunku wyznaczamy optymalną długość kroku 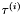$\tau^{(i)}$ i wykonujemy krok próbny wzdłuż i-tej osi:

$\tau^{(i)} = \arg \min_{\tau^{(i)}} f(x^k_{min} + \tau^{(i)} d^{(i)}) .$

$x^i = x^k_{min} + \tau^{(i)} d^{(i)} .$

Zapamiętujemy punkt próbny jako najlepszy:

$x^k_{min} = x^i,$

a następnie przechodzimy do kroku 2.

Krok 2:
Sprawdzamy, czy wykonano kroki próbne we wszystkich kierunkach:
Jeśli 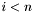$i < n$ , podstawiamy 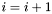$i = i + 1$ i ponownie przechodzimy do kroku 1.
Jeśli 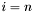$i = n$ , przechodzimy do kroku 3.

Krok 3:
Zapamiętujemy aktualny punkt jako punkt bazowy dla następnego etapu:

$x_b^{k+1} = x^k_{min}.$

Wyznaczamy kierunek kroku roboczego:

$d = x^k_{min} - x_b^k$

i wykonujemy krok roboczy o optymalnej długości w tym kierunku:

$\tau = \arg \min_{\tau} f(x^k_{min} + \tau d) .$

$x^{k+1}_{min} = x^k_{min} + \tau d .$

Przechodzimy do kroku 4.

Krok 4:
Sprawdzamy warunek stopu:
Jeśli jest on spełniony, kończymy działanie. Wynikiem jest 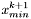$x^{k+1}_{min}$ .
W przeciwnym wypadku podstawiamy 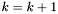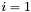$k = k+1$ , $i = 1$ i przechodzimy do kroku 1.

Zobacz również:: HookeJeevesDiscrete, StandardStopCondition

Niniejszy dokument został półautomatycznie wycięty z dokumentacji kodu źródłowego programu Eduoptim 2. Pełna dokumentacja dostępna jest wraz ze źródłami bądź osobno w dziale pliki.
Hierarchia klas w programie nie odpowiada klasyfikacji metod optymalizacji.