#include <RosenbrockOptimal.h>
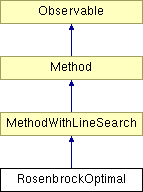
Diagram dziedziczenia dla RosenbrockOptimal

Metoda poszukiwań prostych.
Podobnie jak metoda Rosenbrocka z krokiem dyskretnym, polega na przeszukiwaniu w każdej iteracji 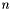 ortogonalnych kierunków i obracaniu bazy w taki sposób, aby nowe kierunki były kierunkami największej dotychczasowej poprawy. W odróżnieniu od pierwotnego wariantu metody Rosenbrocka, w metodzie z krokiem optymalnym wzdłuż każdego z kierunków wykonywany jest tylko jeden krok - krok o optymalnej długości wyznaczonej przez metodę optymalizacji w kierunku. Dzięki temu każdy krok próbny jest krokiem udanym (kończącym się w punkcie o mniejszej niż poprzednio wartości funkcji celu). Upraszcza to znacznie procedurę.
ortogonalnych kierunków i obracaniu bazy w taki sposób, aby nowe kierunki były kierunkami największej dotychczasowej poprawy. W odróżnieniu od pierwotnego wariantu metody Rosenbrocka, w metodzie z krokiem optymalnym wzdłuż każdego z kierunków wykonywany jest tylko jeden krok - krok o optymalnej długości wyznaczonej przez metodę optymalizacji w kierunku. Dzięki temu każdy krok próbny jest krokiem udanym (kończącym się w punkcie o mniejszej niż poprzednio wartości funkcji celu). Upraszcza to znacznie procedurę.
Informacje wejściowe:
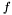 - minimalizowana funkcja
- minimalizowana funkcja 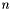 zmiennych,
zmiennych,
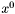 - dowolnie wybrany punkt startowy,
- dowolnie wybrany punkt startowy,
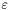 - dokładność właściwego warunku stopu,
- dokładność właściwego warunku stopu,
warunek stopu - do wyboru:
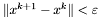 ,
, 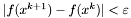 ,
, 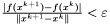 ,
,
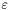 - minimalna długość kroku w całym etapie,
- minimalna długość kroku w całym etapie,
wybrana metoda minimalizacji w kierunku wraz z parametrami.
Oznaczenia:
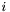 - indeks aktualnego kierunku,
- indeks aktualnego kierunku,
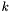 - numer aktualnej iteracji,
- numer aktualnej iteracji,
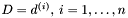 - aktualna baza kierunków,
- aktualna baza kierunków,
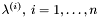 - wektor sum długości udanych kroków próbnych w poszczególnych kierunkach,
- wektor sum długości udanych kroków próbnych w poszczególnych kierunkach,
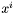 - aktualny punkt próbny,
- aktualny punkt próbny,
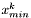 - najlepszy punkt w k-tym etapie,
- najlepszy punkt w k-tym etapie,
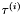 - optymalna długość kroku w i-tym kierunku,
- optymalna długość kroku w i-tym kierunku,
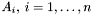 - wektory sum przesunięć wykorzystywane przy obrocie bazy,
- wektory sum przesunięć wykorzystywane przy obrocie bazy,
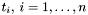 - kwadraty norm wektorów
- kwadraty norm wektorów 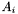 wykorzystywane przy normalizacji nowej bazy (
wykorzystywane przy normalizacji nowej bazy (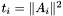 ).
).
Procedura.
Krok wstępny:
Podstawiamy:
![\[ D = I(n), \mbox{ gdzie } I(n) - \mbox{ macierz jednostkowa } n \times n , \]](form_213.png)
![\[ \lambda = 0(n), \]](form_427.png)
![\[ x^1_{min} = x^0, \]](form_214.png)
![\[ k = 1 , \]](form_218.png)
![\[ i = 1 . \]](form_219.png)
Krok 1:
Przy pomocy metody optymalizacji w kierunku wyznaczamy optymalną długość kroku 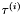 i wykonujemy krok:
i wykonujemy krok:
![\[ \tau^{(i)} = \arg \min_{\tau^{(i)}} f(x^k_{min} + \tau^{(i)} D^{(i)}) . \]](form_475.png)
![\[ x^i = x^k_{min} + \tau^{(i)} D^{(i)} . \]](form_431.png)
Zapamiętujemy długość kroku i aktualny punkt:
![\[ \lambda^{(i)} = \tau^{(i)} , \]](form_476.png)
![\[ x^k_{min} = x^i . \]](form_459.png)
Podstawiamy 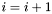 i sprawdzamy, czy
i sprawdzamy, czy 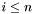 . Jeśli tak, ponownie wykonujemy krok 1. Jeśli nie, podstawiamy
. Jeśli tak, ponownie wykonujemy krok 1. Jeśli nie, podstawiamy 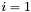 i przechodzimy do kroku 2.
i przechodzimy do kroku 2.
Krok 2:
Sprawdzamy warunek stopu. Jeśli jest on spełniony, to STOP. Wynikiem jest 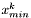 .
.
W przeciwnym wypadku przechodzimy do kroku 3.
Krok 3:
Dokonujemy obrotu bazy, według algorytmu Palmera:
1) Dla 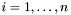 :
:
Wyliczamy wektory sum przesunięć:
![\[ A_i = \sum_{j=i}^n \lambda^{(j)} D^{(j)} \]](form_442.png)
oraz wektor 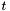 :
:
![\[ t_i = \|A_i\|^2 . \]](form_444.png)
2) Tworzymy nowe kierunki ortonormalne 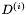 :
:
a) Dla 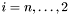 :
:
![\[ div = \sqrt{t_{i-1} t_i} . \]](form_447.png)
![\[ \mbox{Jesli } div \ne 0 : D^{(i)} = \frac{\lambda^{(i-1)} A_i - D^{(i-1)} t_i}{div} , \]](form_448.png)
b) Na koniec tworzymy kierunek największej poprawy 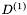 .
.
![\[ div = \sqrt{t_1} , \]](form_449.png)
![\[ D^{(1)} = \frac{A_1}{div}. \]](form_450.png)
W ten sposób otrzymujemy nową bazę kierunków 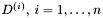 .
.
Następnie podstawiamy:
![\[ \lambda = 0(n), \]](form_427.png)
![\[ k = k + 1 \]](form_454.png)
i przechodzimy do kroku 1.
Uwagi.
Oryginalna metoda Rosenbrocka wykorzystywała przy ortonormalizacji nowej bazy metodę Grama-Schmidta. W tej implementacji użyto metody Palmera, bardziej wydajnej i tworzącej poprawną bazę również w przypadku, gdy w iteracji istnieją kierunki, w których nie wykonano żadnego udanego kroku.